Решебник по геометрии 11 класс. Атанасян ФГОС 145

\[\boxed{\mathbf{145.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

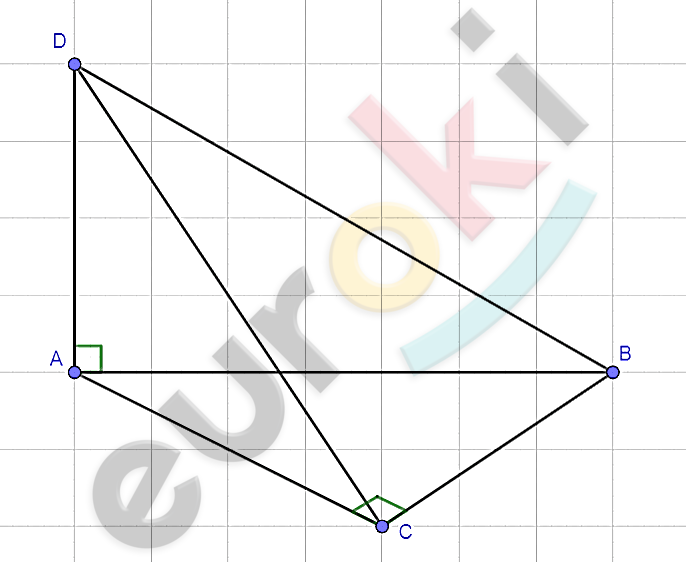
\[\mathrm{\Delta}ABC - прямоугольный;\]

\[AD\bot ABC;\]

\[\textbf{б)}\ BC = a;\]

\[DC = b.\]

\[Доказать:\]

\[\textbf{а)}\ \mathrm{\Delta}CBD - прямоугольный.\]

\[Найти:\]

\[\textbf{б)}\ BD.\]

\[Решение.\]

\[1)\ AD - перпендикуляр\ к\ \]

\[плоскости\ ABC;\]

\[DC - наклонная;\]

\[AC - проекция\ \text{DC\ }на\ \]

\[плоскости\ \text{ABC.}\]

\[\textbf{а)}\ Если\ \angle C = 90{^\circ},\ то\ CB\bot CA:\ \]

\[прямая\ \text{CB\ }перпендикулярна\ к\ \]

\[проекции\ \text{AC\ }прямой\ \text{DC.}\]

\[По\ теореме\ о\ трех\ \]

\[перпендикулярных\ прямых:\]

\[\ BC\ перпендикулярна\ и\ к\ DC;\ \]

\[\angle DCB = 90{^\circ}.\]

\[Отсюда:\]

\[\mathrm{\Delta}DCB - прямоугольный.\]

\[Что\ и\ требовалось\ доказать.\]

\[\textbf{б)}\ \mathrm{\Delta}DCB - прямоугольный:\]

\[BD^{2} = DC^{2} + CB^{2};\]

\[BD = \sqrt{a^{2} + b^{2}}.\]

\[Ответ:\ \sqrt{a^{2} + b^{2}}.\ \]