Решебник по геометрии 10 класс Атанасян ФГОС 88

\[\boxed{\mathbf{88.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[AA \parallel BD;\]

\[AC \cap \alpha = A;\]

\[BD \cap \alpha = B;\]

\[AC = 8\ см;\]

\[BD = 6\ см;\]

\[AB = 4\ см.\]

\[Доказать:\]

\[CD \cap \alpha = E.\]

\[Найти:\]

\[BE - ?\]

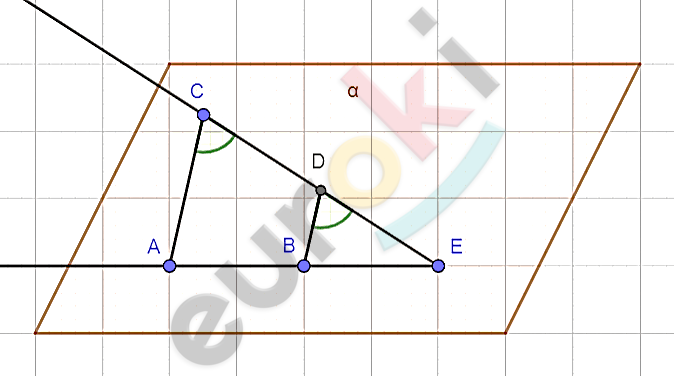
\[Решение.\]

\[1)\ Так\ как\ AC \parallel BD\ и\ \text{AC} \neq BD,\ \]

\[то\ ABCD - трапеция;\]

\[CD,AB - боковые\ стороны:\]

\[\ CD \nparallel BD\ и\ точки\ ABCD -\]

\[лежат\ в\ одной\ плоскости\ \]

\[\text{ABCD.\ }\]

\[Отсюда:\]

\[DC \cap AB.\]

\[2)\ ABC \cap \alpha = AB,\ CD \in ABC\ и\ \]

\[DC \cap AB:\]

\[DC \cap \alpha = E.\]

\[Что\ и\ требовалось\ доказать.\]

\[3)\ \mathrm{\Delta}EDC\sim\mathrm{\Delta}ECA:\]

\[\angle E - общий;\]

\[\angle C = \angle D\ \]

\[(как\ соответственные)\]

\[Отсюда:\]

\[BE\ :AE = DB\ :AC.\]

\[4)\ AE = AB + BE = 4 + BE\]

\[BE\ :(BE + 4) = 6\ :8\]

\[8 \bullet BE = 24 + 6 \bullet BE\]

\[2BE = 24\]

\[BE = 12\ см.\]

\[Ответ:12\ см.\]