Решебник по геометрии 10 класс Атанасян ФГОС 858

\[\boxed{\mathbf{858.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\ \ \]

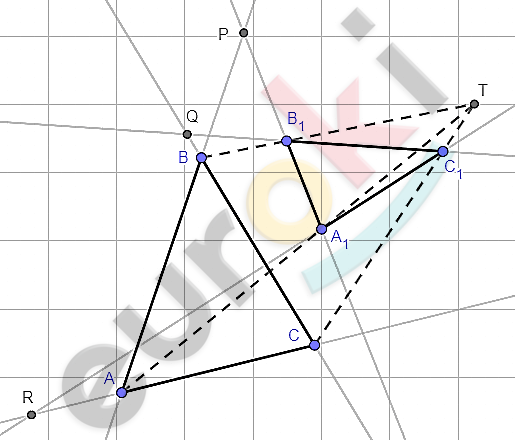
\[\mathrm{\Delta}ABC\ и\ \mathrm{\Delta}A_{1}B_{1}C_{1};\ \ \]

\[BC \cap B_{1}C_{1} = Q;\ \ \]

\[AB \cap A_{1}B_{1} = P;\ \ \]

\[CA \cap C_{1}A_{1} = R.\]

\[Доказать:\ \ \]

\[AA_{1},BB_{1},CC_{1}\ пересекаются\ в\ \]

\[одной\ точке\ или\ параллельны,\]

\[только\ тогда,\ когда\ P,Q\ и\ R -\]

\[лежат\ на\ одной\ прямой.\]

\[Доказательство.\]

\[Пусть\ AA_{1},BB_{1}\ и\ CC_{1}\ \]

\[пересекаются\ в\ одной\ точке\ \text{T.}\]

\[По\ теореме\ Менелая\]

\[1)\ для\ \mathrm{\Delta}ABT:\ \]

\[\frac{\text{AP}}{\text{BP}} \bullet \frac{BB_{1}}{TB_{1}} \bullet \frac{TA_{1}}{AA_{1}} = 1\ \]

\[\begin{pmatrix} так\ как\ точки\ P,B_{1}\ и\ A_{1}\ \ \\ принадлежат\ одной\ прямой \\ \end{pmatrix};\ \]

\[2)\ для\ \mathrm{\Delta}AСT:\ \]

\[\frac{\text{AR}}{\text{CR}} \bullet \frac{CC_{1}}{TC_{1}} \bullet \frac{TA_{1}}{AA_{1}} = 1\ \]

\[\begin{pmatrix} так\ как\ точки\ R,C_{1}\ и\ A_{1}\ \ \\ принадлежат\ одной\ прямой \\ \end{pmatrix};\]

\[3)\ для\ \mathrm{\Delta}BCT:\ \]

\[\frac{\text{BQ}}{\text{CQ}} \bullet \frac{CC_{1}}{TC_{1}} \bullet \frac{TB_{1}}{BB_{1}} = 1\ \]

\[\begin{pmatrix} так\ как\ точки\ Q,C_{1}\ и\ B_{1}\ \ \\ принадлежат\ одной\ прямой \\ \end{pmatrix}.\]

\[Таким\ образом:\]

\[\frac{\text{AP}}{\text{BP}} \bullet \frac{\text{BQ}}{\text{CQ}} \bullet \frac{\text{CR}}{\text{AR}} =\]

\[= \frac{TB_{1} \bullet AA_{1}}{BB_{1} \bullet TA_{1}} \bullet \frac{TC_{1} \bullet BB_{1}}{CC_{1} \bullet TB_{1}} \bullet \frac{CC_{1} \bullet TA_{1}}{TC_{1} \bullet AA_{1}} =\]

\[= 1.\]

\[Следовательно:\]

\[точки\ P,Q\ и\ R - лежат\ на\ \]

\[одной\ прямой.\]

\[Аналогично\ при\ обратном\ \]

\[доказательстве.\]

\[Что\ и\ требовалось\ доказать.\]