Решебник по геометрии 10 класс Атанасян ФГОС 851

\[\boxed{\mathbf{851.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

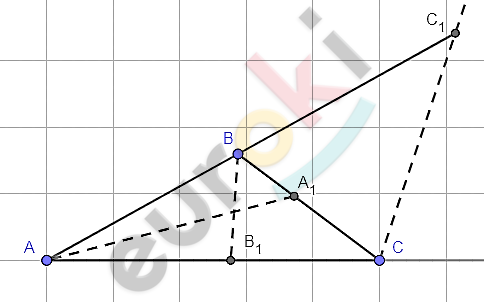
\[\mathrm{\Delta}ABC;\]

\[AA_{1},BB_{1} - биссектрисы;\]

\[CC_{1} - биссектриса\ внешнего\ \]

\[угла;\]

\[C_{1} \in AB.\]

\[Доказать:\]

\[A_{1},B_{1},C_{1} - лежат\ на\ одной\ \]

\[прямой.\]

\[Доказательство.\]

\[1)\ По\ свойству\ биссектрисы:\ \ \]

\[\frac{CB_{1}}{AB_{1}} = \frac{\text{CB}}{\text{AB}};\text{\ \ }\]

\[\frac{BA_{1}}{CA_{1}} = \frac{\text{AB}}{\text{AC}}.\]

\[2)\ Из\ решения\ задачи\ 837:\ \ \]

\[\frac{AC_{1}}{BC_{1}} = \frac{\text{AC}}{\text{CB}}.\]

\[3)\ Таким\ образом:\]

\[\frac{AC_{1}}{BC_{1}} \bullet \frac{BA_{1}}{CA_{1}} \bullet \frac{CB_{1}}{AB_{1}} = \frac{\text{AC}}{\text{CB}} \bullet \frac{\text{AB}}{\text{AC}} \bullet \frac{\text{CB}}{\text{AB}} =\]

\[= 1.\]

\[Следовательно,\ по\ теореме\ \]

\[Менелая:\ \ \]

\[точки\ A_{1},B_{1}\ и\ C_{1}\ лежат\ на\ \]

\[одной\ прямой.\]

\[Что\ и\ требовалось\ доказать.\]