Решебник по геометрии 10 класс Атанасян ФГОС 810

\[\boxed{\mathbf{810.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[шар\ (O;R);\]

\[описанный\ конус;\]

\[\angle AMB = a.\]

\[Найти:\]

\[\text{a.}\]

\[Решение.\]

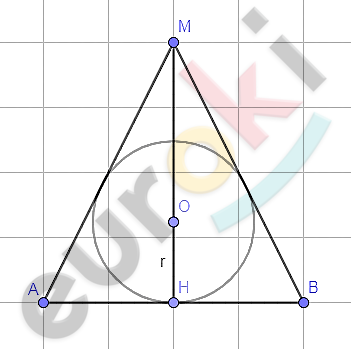
\[1)\ Рассмотрим\ осевое\ сечение\ \]

\[конуса\ AMB.\]

\[Опустим\ высоту\ MH\bot AB.\]

\[AM = MB:\]

\[\mathrm{\Delta}AMB - равносторонний;\]

\[OH - радиус\ вписанной\ в\ \]

\[\mathrm{\Delta}AMB\ окружности.\]

\[2)\ S_{\text{AMB}} =\]

\[= \frac{1}{2}(AB + MA + MB) \bullet OH =\]

\[= \frac{1}{2}AB \bullet MH:\]

\[(AH + MA) \bullet OH = AH \bullet MH;\]

\[\left( AH + \sqrt{MH^{2} + AH^{2}} \right) \bullet OH =\]

\[= AH \bullet MH;\]

\[\text{OH}\left( \sqrt{MH^{2} + AH^{2}} \right) =\]

\[= AH \bullet (MH - OH);\]

\[AH^{2} = \frac{OH^{2} \bullet MH}{MH - 2OH}.\]

\[3)\ Объем\ конуса\ \]

\[(AH - радиус\ основания):\]

\[V = \frac{1}{3}\pi \bullet AH^{2} \bullet MH =\]

\[= \frac{1}{3}\pi \bullet \frac{MH^{2} \bullet OH^{2}}{MH - 2OH}.\]

\[Производная:\]

\[V^{'} =\]

\[= \frac{1}{3}\pi \bullet OH^{2} \bullet \frac{2MH(MH - 2OH) - MH^{2}}{(MH - 2OH)^{2}}\]

\[2MH(MH - 2OH) - MH^{2} = 0\]

\[MH = 4OH.\]

\[4)\ При\ MH < 4OH \rightarrow V^{'} < 0;\ \ \]

\[MH > 4OH = > V^{'} > 0.\]

\[объем\ \text{V\ }имеет\ минимальное\ \]

\[значение:\]

\[AH^{2} = 2OH^{2}\text{\ \ }\]

\[AM = \sqrt{MH^{2} + AH^{2}} = 3OH\sqrt{2};\]

\[\angle AMH = \frac{1}{2}\angle AMB = \frac{1}{2}\text{a.}\]

\[5)\ В\ \mathrm{\Delta}AMH - прямоугольном:\]

\[\sin\frac{a}{2} = \frac{\text{AH}}{\text{AM}} = \frac{\text{OH}\sqrt{2}}{3OH\sqrt{2}} = \frac{1}{3}\]

\[a = 2\arcsin\frac{1}{3}.\]

\[\mathbf{Ответ}\mathbf{:\ }\text{\ a}\mathbf{=}2\arcsin\frac{1}{3}.\]