Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 10 класс Атанасян ФГОС 808
808
\[\boxed{\mathbf{808.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]
\[Дано:\ \ \]
\[плоскости\ \alpha \parallel \beta.\ \]
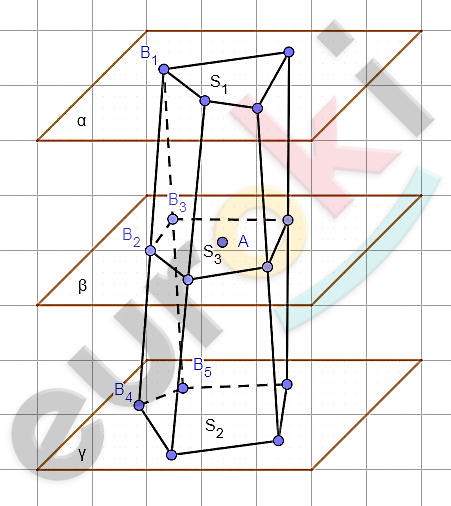
\[Доказать:\ \text{\ \ }\]
\[V = \frac{h}{6}\left( S_{1} + S_{2} + 4S_{3} \right).\]
\[Доказательство.\]
\[1)\ Возьмем\ точку\ \text{A\ }внутри\ \]
\[сечения\ многогранника\ \]
\[плоскостью\ S_{3};\]
\[разобьем\ многогранник\ на\ \]
\[пирамиды,\ вершиной\ которых\ \]
\[является\ точка\ A,\ а\ \]
\[основаниями - основания\ и\ \]
\[боковые\ стороны\ \]
\[многогранника.\]
\[2)\ Найдем\ объем\ пирамид,\]
\[основаниями\ которых\ \]
\[являются\ основания\ \]
\[многогранника\ (плоскость\ \gamma\ \]
\[равноудаленна\ от\ \alpha\ и\ \beta;\ \]
\[высота\ пирамид\ равна\ \frac{h}{2}):\ \ \ \ \]
\[V_{1} = \frac{1}{3} \bullet S_{1} \bullet \frac{h}{2} = \frac{S_{1}h}{6};\text{\ \ }\]
\[V_{2} = \frac{1}{3} \bullet S_{2} \bullet \frac{h}{2} = \frac{S_{2}h}{6}.\]
\[3)\ Рассмотрим\ одну\ из\ \]
\[боковых\ треугольных\ граней.\]
\[Плоскость\ S_{3}\ равноудалена\ от\ \]
\[S_{1}\ и\ S_{2}:\]
\[S_{3}\ пересекает\ грань\ B_{4}B_{5}B_{1}\ по\ \]
\[средней\ линии\ B_{2}B_{3}.\]
\[Тогда:\ \]
\[S_{B_{1}B_{2}B_{3}} = \frac{1}{4}S_{B_{1}B_{4}B_{5}};\]
\[\ V_{A{B_{1}B}_{2}B_{3}} = \frac{1}{3}S_{AB_{2}B_{3}} \bullet \frac{1}{2}h =\]
\[= \frac{1}{6}S_{AB_{2}B_{3}}\]
\[V_{AB_{1}B_{2}B_{3}} = \frac{1}{3} \bullet S_{B_{1}B_{4}B_{5}} \bullet h_{1};\]
\[\ где\ h_{1} - высота,\ опущенная\ из\ \]
\[точки\ \text{A\ }на\ плоскость\ B_{1}B_{4}B_{5}.\]
\[V_{AB_{2}B_{3}B_{4}B_{5}} = \frac{1}{3} \bullet S_{B_{1}B_{4}B_{5}} \bullet h_{1} =\]
\[= \frac{1}{3} \bullet 4 \bullet S_{B_{1}B_{2}B_{3}} \bullet h_{1} = 4\ V_{A{B_{1}B}_{2}B_{3}}.\]
\[Тогда:\]
\[V_{AB_{2}B_{3}B_{4}B_{5}} = \frac{4}{6}S_{AB_{2}B_{3}} \bullet h.\]
\[4)\ Все\ грани\ многогранника,\ \]
\[являющиеся\ \]
\[четырехугольниками,можно\ \]
\[также\ разбить\ на\ \]
\[треугольники,\ тогда\ суммой\ \]
\[площадей\ всех\ оснований\ \]
\[таких\ пирамид\ будет\ являться\ \]
\[площадь\ сечения\ S_{3},\ а\ их\ \]
\[общий\ объем:\ \ \]
\[V_{3} = \frac{4}{6}h \bullet S_{3}.\]
\[5)\ Объем\ многогранника\ \]
\[равен:\]
\[V = V_{1} + V_{2} + V_{3} =\]
\[= \frac{S_{1}h}{6} + \frac{S_{2}h}{6} + \frac{{4S}_{3}h}{6} =\]
\[= \frac{h}{6}\left( S_{1} + S_{2} + 4S_{3} \right).\ \]
\[Что\ и\ требовалось\ доказать.\]
