Решебник по геометрии 10 класс Атанасян ФГОС 805

\[\boxed{\mathbf{805.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\ \ \]

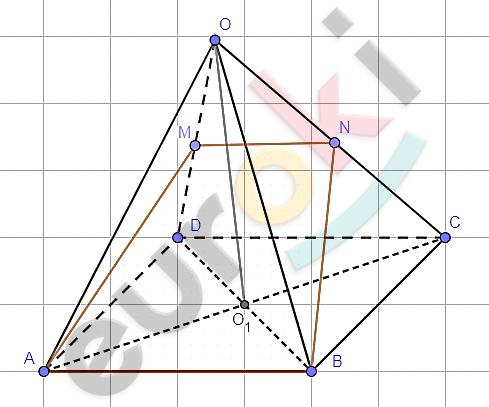
\[OABCD - пирамида;\ \ \]

\[ABMD - сечение;\ \ \]

\[OM = MD;\text{\ \ }\]

\[ON = NC.\]

\[Найти:\ \text{\ \ }\]

\[V_{\text{ABMNO}}\ :V_{\text{ABCDMN}}.\]

\[Решение.\]

\[1)\ Опустим\ высоты\ из\ токи\ \text{O\ }\]

\[на\ плоскость\ ABCD:\ \ \]

\[OO_{1}\bot ABCD.\]

\[Пусть\ V_{\text{ABCDO}} = V.\]

\[2)\ S_{\text{ABC}} = \frac{1}{2}S_{\text{ABCD}};\text{\ \ }\]

\[NN_{1} = \frac{1}{2}\text{\ O}O_{1}:\]

\[V_{\text{ABCN}} = \frac{1}{4}\text{V.}\]

\[3)\ S_{\text{BNO}} = S_{\text{BCN}}\ \]

\[(так\ как\ BN - медиана\ \mathrm{\Delta}OBC);\]

\[высота,\ опущенная\ из\ точки\ \text{A\ }\]

\[на\ плоскость\ OBC - общая:\ \]

\[V_{\text{ABNO}} = V_{\text{ABCN}} = \frac{1}{4}\text{V.}\]

\[4)\ S_{\text{ACD}} = \frac{1}{2}S_{\text{ABCD}};\ \]

\[высота\ OO_{1} - общая:\ \]

\[V_{\text{AOCD}} = \frac{1}{2}\text{V.}\]

\[5)\ S_{\text{OMN}} = \frac{1}{4}S_{\text{OCD}}\ \]

\[(так\ как\ MN - средняя\ линия\ \mathrm{\Delta}OCD);\]

\[высота\ из\ точки\ \text{A\ }на\ плоскость\ \]

\[\text{OCD\ }общая:\]

\[V_{\text{AOMN}} = \frac{1}{4}V_{\text{AOCD}} = \frac{1}{8}\text{V.}\]

\[6)\ Найдем\ отношение\ объемов:\]

\[V_{\text{ABMNO}} = V_{\text{AOMN}} + V_{\text{ABNO}} =\]

\[= \frac{1}{8}V + \frac{1}{4}V = \frac{3}{8}V;\]

\[V_{\text{ABCDMN}} = V - V_{\text{ABMNO}} =\]

\[= V - \frac{3}{8}V = \frac{5}{8}V;\]

\[V_{\text{ABMNO}}\ :V_{\text{ABCDMN}} = 3\ :5.\]

\[Ответ:\ \ 3\ :5.\]