Решебник по геометрии 10 класс Атанасян ФГОС 790

\[\boxed{\mathbf{790.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\ \ \]

\[OABC - тетраэдр;\ \ \ \]

\[\mathrm{\Delta}ABC - основание;\ \]

\[\ все\ углы\ при\ \ вершине\ \]

\[O - прямые.\]

\[Доказать:\]

\[луч\ света,\ вошедший\ в\ \]

\[тетраэдр\ через\ основание\ ABC,\ \]

\[отразившись,\ выйдет\ в\ \]

\[противоположном\ \]

\[направлении.\]

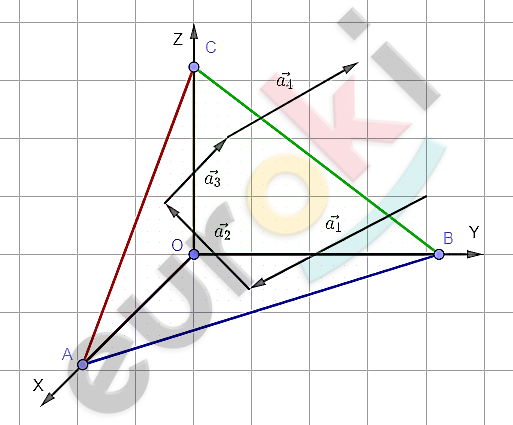
\[Доказательство.\]

\[1)\ Введем\ систему\ координат,\ \]

\[направим\ оси:\ \ \]

\[OX - вдоль\ OA;\]

\[OY - вдоль\ OB;\ \ \]

\[OZ - вдоль\ \text{OC.}\]

\[2)\ Пусть\ {\overrightarrow{a}}_{1}\left\{ x,y,z \right\} -\]

\[направляющий\ вектор\ \]

\[падающего\ луча.\]

\[3)\ Если\ луч\ падает\ на\ плоскость\ \]

\[\text{AOB\ }под\ некоторым\ углом,\ то\]

\[направляющий\ вектор\ \]

\[отраженного\ луча\ {\overrightarrow{a}}_{2}\left\{ x,y, - z \right\}.\]

\[4)\ Луч\ продолжит\ движение\ и\ \]

\[упадет\ на\ грань\ OAC,\ тогда\]

\[направляющий\ вектор\ \]

\[отраженного\ луча\ {\overrightarrow{a}}_{3}\left\{ x, - y, - z \right\}.\]

\[5)\ Когда\ луч\ упадет\ на\ грань\ \]

\[OCB,\ направляющий\ вектор\ \]

\[отраженного\ луча\ станет\ \]

\[равным\ {\overrightarrow{a}}_{4}\left\{ - x, - y, - z \right\}\text{\ \ }\]

\[(аналогично\ при\ любом\ \]

\[порядке\ отражения\ луча\ от\ \]

\[граней).\]

\[6)\ Отразившись\ от\ всех\ граней,\ \]

\[луч\ выйдет\ по\ направляющему\ \]

\[вектору\]

\[{\overrightarrow{a}}_{4}\left\{ - x, - y, - z \right\} = - {\overrightarrow{a}}_{1}\left\{ x,y,z \right\}.\]

\[Что\ и\ требовалось\ доказать.\]