Решебник по геометрии 10 класс Атанасян ФГОС 785

\[\boxed{\mathbf{785.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\ \]

\[A_{1}A_{2}\ldots A_{20} - правильный\ \]

\[додекаэдр;\ \ \]

\[O_{1}O_{2}\ldots O_{12} - центры\ граней\text{.\ \ }\]

\[Доказать:\ \]

\[O_{1}O_{2}\ldots O_{12} - правильный\ \]

\[икосаэдр.\]

\[Доказательство.\]

\[1)\ Прямая,\ соединяющая\ две\ \]

\[противоположные\ вершины\ \]

\[правильного\ додекаэдра,\ \]

\[является\ \ осью\ симметрии\ \]

\[третьего\ порядка:\ додекаэдр\ \]

\[совмещается\ с\ собой\ при\ \]

\[повороте\ на\ 120{^\circ}\ или\ 240{^\circ}.\]

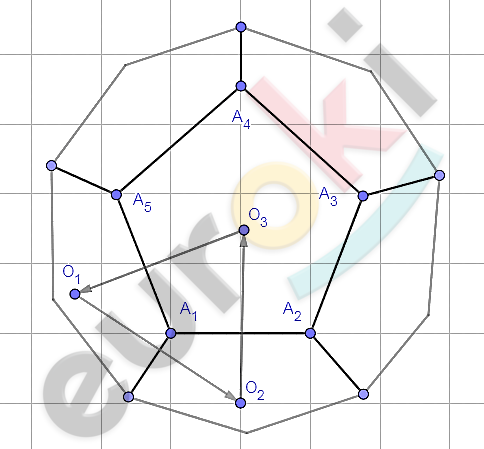
\[2)\ Пусть\ додекаэр\ вращается\ \]

\[вокруг\ оси,\ проходящей\ через\ \]

\[вершину\ A_{1},\ тогда\ при\ \]

\[повороте\ на\ 120{^\circ}:\]

\[O_{1} \rightarrow O_{2};\ \ O_{2} \rightarrow O_{3};\ O_{3} \rightarrow O_{1}\text{.\ }\]

\[Следовательно:\ \]

\[\mathrm{\Delta}O_{1}O_{2}O_{3} - правильный.\]

\[3)\ Аналогично\ для\ осей,\ \]

\[проходящих\ через\ каждую\ \]

\[вершину\ додекаэдра:каждые\ \]

\[точки\ центров\ трех\ соседних\ \]

\[граней\ додекаэдра\ образуют\ \]

\[правильный\ треугольник.\]

\[4)\ Таким\ образом:\ \]

\[12\ точек\ центров\ граней\ \]

\[додекаэдра\ образуют\ 20\ \]

\[правильных\ ⊿.\]

\[Следовательно:\ O_{1}O_{2}\ldots O_{12} -\]

\[правильный\ икосаэдр.\]

\[Что\ и\ требовалось\ доказать.\]