Решебник по геометрии 10 класс Атанасян ФГОС 722

\[\boxed{\mathbf{722.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[\textbf{а)}\]

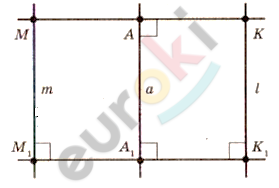
\[Пусть\ прямая\ a - ось\ \]

\[симметрии;\ \ l \parallel a.\]

\[Из\ точки\ K \in l\ проведен\ \]

\[перпендикуляр:\]

\[KA\bot a;\]

\[KA = AM.\]

\[Из\ точки\ K_{1} \in l\ проведем\ \]

\[K_{1}A_{1}\bot a;\ \ A_{1}M_{1} = K_{1}A_{1}.\]

\[Прямые\ a\ и\ \text{l\ }лежат\ в\ одной\ \]

\[плоскости:\]

\[\text{KM}M_{1}K_{1} - плоский\ \]

\[четырехугольник.\]

\[MK = M_{1}K_{1};\ \ MK\bot l;\ \ M_{1}K_{1}\bot l:\]

\[MK \parallel M_{1}K_{1};\]

\[\text{MK}K_{1}M_{1} - прямоугольник;\]

\[m \parallel l.\]

\[Что\ и\ требовалось\ доказать.\]

\[\textbf{б)}\ \]

\[Если\ прямая\ a \nparallel l:\]

\[a\ пересекается\ с\ прямой\ в\ \]

\[точке\ \text{A.}\]

\[Пусть\ N \in l;NO\bot a;NO = OK.\]

\[Через\ точку\ K\ проведем\ \]

\[прямую\ \text{KA.}\]

\[⊿AOK = ⊿AON:\]

\[NO = OK;\]

\[AO - общий\ катет.\]

\[Значит,\ прямая\ \text{KA\ }образует\ \]

\[угол\ \text{φ\ }с\ осью\ симметрии:\]

\[\varphi = \angle AON = \angle OAK.\]

\[Что\ и\ требовалось\ доказать.\]