Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 10 класс Атанасян ФГОС 703
703
\[\boxed{\mathbf{703.}еуроки - ответы\ на\ пятёрку}\]
\[Дано:\]
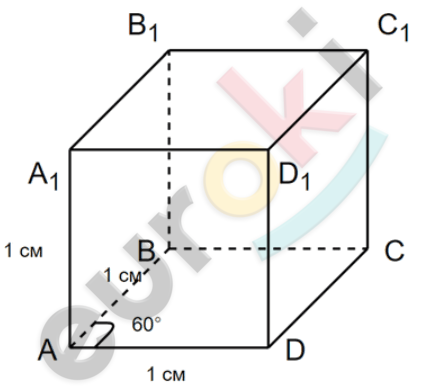
\(AA_{1} = AB = AD = 1;\)
\[\angle DAB = 60{^\circ};\]
\[\angle A_{1}AD = \angle A_{1}AB = 90{^\circ}.\]
\[Решение.\]
\[1)\cos{\angle\left( \overrightarrow{a}\overrightarrow{b} \right)} = \frac{\overrightarrow{a} \cdot \overrightarrow{b}}{\left| \overrightarrow{a} \right| \cdot \left| \overrightarrow{b} \right|};\]
\[\overrightarrow{a} \cdot \overrightarrow{b} = \cos{\angle\left( \overrightarrow{a}\overrightarrow{b} \right)} \cdot \left| \overrightarrow{a} \right| \cdot \left| \overrightarrow{b} \right|.\]
\[2)\ По\ теореме\ Пифагора:\]
\[DC_{1} = AB_{1} = CD_{1} = BA_{1} =\]
\[= BC_{1} = CB_{1} = AD_{1} = DA_{1} =\]
\[= \sqrt{2}.\]
\[3)\ По\ теореме\ косинусов:\]
\[AC = A_{1}C_{1} = \sqrt{3};\]
\[BD = B_{1}D_{1} = 1.\]
\[\textbf{а)}\ \overrightarrow{\text{BA}} \cdot \overrightarrow{D_{1}C_{1}} = \cos{180{^\circ}} \cdot 1 \cdot 1 =\]
\[= - 1.\]
\[\textbf{б)}\ \overrightarrow{BC_{1}} \cdot \overrightarrow{D_{1}B} =\]
\[= \overrightarrow{BC_{1}} \cdot \left( \overrightarrow{D_{1}C_{1}} + \overrightarrow{C_{1}B_{1}} + \overrightarrow{B_{1}B} \right) =\]
\[= \frac{1}{2} - 0 - 1 - 1 = - \frac{3}{2}.\]
\[\textbf{в)}\ \overrightarrow{AC_{1}} \cdot \overrightarrow{AC_{1}} =\]
\[= \left( \overrightarrow{\text{AC}} + \overrightarrow{CC_{1}} \right)\left( \overrightarrow{\text{AC}} + \overrightarrow{CC_{1}} \right) =\]
\[= \overrightarrow{\text{AC}} \cdot \overrightarrow{\text{AC}} + 2\overrightarrow{\text{AC}} \cdot \overrightarrow{CC_{1}} + \overrightarrow{CC_{1}} \cdot \overrightarrow{CC_{1}} =\]
\[= \sqrt{3} \cdot \sqrt{3} + 2 \cdot \cos{90{^\circ}} \cdot \sqrt{3} + 1 \cdot 1 =\]
\[= 4.\]
\[\textbf{г)}\ По\ теореме\ Пифагора:\]
\[\left| \overrightarrow{\text{DB}_{1}} \right| = \sqrt{BD^{2} + BB_{1}^{2}} = \sqrt{2}.\]
\[\textbf{д)}\ По\ теореме\ Пифагора:\]
\[\left| \overrightarrow{A_{1}C} \right| = \sqrt{AC^{2} + AA_{1}^{2}} = 2.\]
\[\textbf{е)}\cos{\angle\left( \overrightarrow{DA_{1}};\overrightarrow{D_{1}B} \right)} =\]
\[= \frac{\overrightarrow{DA_{1}} \cdot \overrightarrow{D_{1}B}}{\sqrt{2} \cdot \sqrt{2}} = \frac{1}{2}\overrightarrow{DA_{1}} \cdot \overrightarrow{D_{1}B} =\]
\[\textbf{ж)}\ Аналогично\ пункту\ е):\]
\[\cos{\angle\left( \overrightarrow{AC_{1}};\overrightarrow{DB_{1}} \right)} =\]
\[= \frac{\overrightarrow{AC_{1}} \cdot \overrightarrow{DB_{1}}}{\left| \overrightarrow{AC_{1}} \right| \cdot \left| \overrightarrow{DB_{1}} \right|} = \frac{\sqrt{2}}{4}.\]
