Решебник по геометрии 10 класс Атанасян ФГОС 7

\[\boxed{\mathbf{7.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

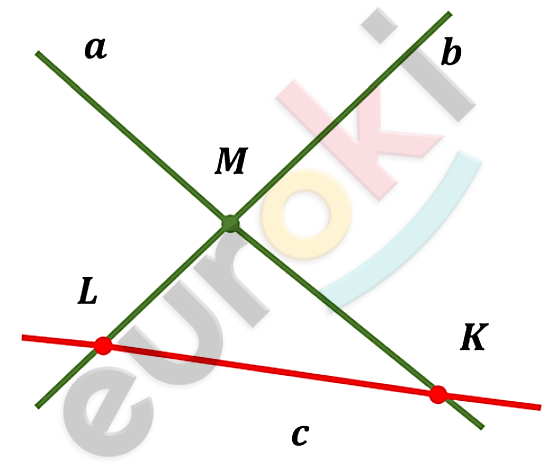
\[M = a \cap b;\]

\[c - прямая;\]

\[K = a \cap c;\ \ K \neq M;\]

\[L = b \cap c;\ \ L \neq M.\]

\[Доказательство.\]

\[1)\ Возьмем\ любую\ прямую\ c_{1}.\]

\[Проведем\ плоскость\ через\ три\ \]

\[точки\ M;L;K\ (аксиома\ 1):\]

\[M \in \alpha;\ \ L \in \alpha;\ \ K \in \alpha.\]

\[Отсюда,\ по\ аксиоме\ 2:\]

\[b \in \alpha;\ \ a \in \alpha.\]

\[2)\ Возьмем\ любую\ другую\ \]

\[прямую,\ пусть\ будет\ c_{2},\ \]

\[удовлетворяющую\ условию\ \]

\[задачи:\]

\[новая\ точка\ L_{2} \in b \subset \alpha;\ \ L_{2} \in \alpha;\]

\[новая\ точка\ K_{2} \in a \subset \alpha;\ \ K_{2} \in a.\]

\[Следовательно,\ по\ аксиоме\ 2:\]

\[c_{2} \subset \alpha.\]

\[Что\ и\ требовалось\ доказать.\]

\[Ответ\ на\ вопрос:\]

\[не\ все\ прямые,\ проходящие\ \]

\[через\ точку\ M,\ лежат\ в\ одной\ \]

\[плоскости:например,\ N \notin \alpha;\ \ \]

\[MN \notin \alpha;\ \ но\ a \subset \alpha;b \subset \alpha.\]