Решебник по геометрии 10 класс Атанасян ФГОС 669

\[\boxed{\mathbf{669.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[A( - 3;4; - 4);\]

\[A_{1}( - 3;4;0) - проекция\ точки\ \]

\[\text{A\ }на\ Oxy;\]

\[A_{2}(0;4; - 4) - проекция\ точки\ \]

\[\text{A\ }на\ Oyz;\]

\[A_{3}( - 3;0; - 4) - проекция\ точки\ \]

\[\text{A\ }на\ \text{Oxz.}\]

\[Формула\ расстояния\ между\ \]

\[точками:\]

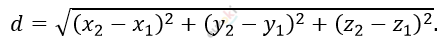
\[\textbf{а)}\ \left| AA_{1} \right| = \left| \overrightarrow{AA_{1}} \right| =\]

\[= \sqrt{( - 3 + 3)^{2} + (4 - 4)^{2} + (0 + 4)^{2}} =\]

\[= \sqrt{16} = 4;\]

\[\left| AA_{2} \right| = \left| \overrightarrow{AA_{2}} \right| =\]

\[= \sqrt{(0 + 3)^{2} + (4 - 4)^{2} + ( - 4 + 4)^{2}} =\]

\[= \sqrt{9} = 3;\]

\[\textbf{б)}\ A_{x}( - 3;0;0);\ \ A_{y}(0;4;0);\ \ \]

\[A_{z}(0;0; - 4):\]

\[\left| \overrightarrow{AA_{x}} \right| = \sqrt{0 + 4^{2} + 4^{2}} = 4\sqrt{2};\]

\[\left| \overrightarrow{AA_{y}} \right| = \sqrt{3^{2} + 0^{2} + 4^{2}} =\]

\[= \sqrt{25} = 5;\]

\[\left| \overrightarrow{AA_{z}} \right| = \sqrt{3^{2} + 4^{2}} = 5.\]