Решебник по геометрии 10 класс Атанасян ФГОС 665

\[\boxed{\mathbf{665.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Формула:\]

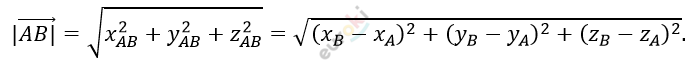
\[\overrightarrow{a}\left\{ 3; - 2;1 \right\};\ \ \overrightarrow{b}\left\{ - 2;3;1 \right\};\ \ \]

\[\overrightarrow{c}\left\{ - 3;2;1 \right\}.\]

\[\textbf{а)}\ \left| \overrightarrow{a} + \overrightarrow{b} \right| =\]

\[= \sqrt{(3 - 2)^{2} + ( - 2 + 3)^{2} + (1 + 1)^{2}} =\]

\[= \sqrt{6}.\]

\[\textbf{в)}\ \left| \overrightarrow{a} \right| - \left| \overrightarrow{b} \right| = \sqrt{14} - \sqrt{14} = 0.\]

\[\textbf{г)}\ \left| \overrightarrow{a} - \overrightarrow{b} \right| =\]

\[= \sqrt{(3 + 2)^{2} + ( - 2 - 3)^{2} + (1 - 1)^{2}} =\]

\[= \sqrt{50} = 5\sqrt{2}.\]

\[\textbf{д)}\ \left| 3\overrightarrow{c} \right| = \sqrt{( - 9)^{2} + 6^{2} + 3^{2}} =\]

\[= \sqrt{126} = 3\sqrt{14}.\]

\[\textbf{е)}\ \sqrt{14}\left| \overrightarrow{c} \right| =\]

\[= \sqrt{14} \cdot \sqrt{( - 3)^{2} + 2^{2} + 1^{2}} =\]

\[= \sqrt{14} \cdot \sqrt{14} = 14.\]

\[\textbf{ж)}\ \left| 2\overrightarrow{a} - 3\overrightarrow{c} \right| =\]

\[= \sqrt{(6 + 9)^{2} + ( - 4 - 6)^{2} + (2 - 3)^{2}} =\]

\[= \sqrt{326}.\]