Решебник по геометрии 10 класс Атанасян ФГОС 632

\[\boxed{\mathbf{632.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\ \ \]

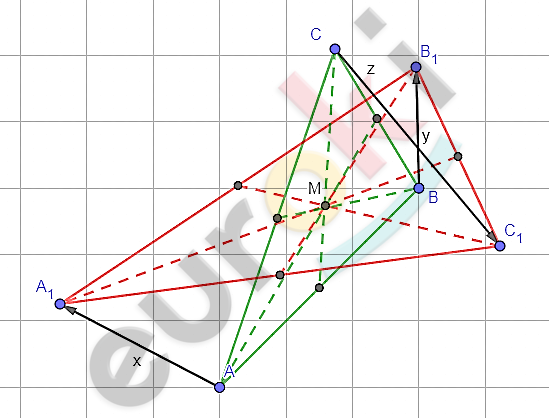
\[\mathrm{\Delta}ABC\ и\ \mathrm{\Delta}A_{1}B_{1}C_{1};\]

\[медианы\ треугольников\ \]

\[пересекаются\ в\ точке\ M.\]

\[Доказать:\ \ \]

\[прямые\text{\ A}A_{1},BB_{1}\ и\ CC_{1}\ \]

\[параллельны\ некоторой\ \]

\[плоскости.\]

\[Доказательство.\]

\[1)\ Пусть\ O - произвольная\ \]

\[точка\ пространства;\ \]

\[\overrightarrow{AA_{1}} = \overrightarrow{x};\ \ \overrightarrow{BB_{1}} = \overrightarrow{y};\ \ \overrightarrow{CC_{1}} = \overrightarrow{z}.\]

\[2)\ \overrightarrow{\text{OM}} = \frac{1}{3}\left( \overrightarrow{\text{OA}} + \overrightarrow{\text{OB}} + \overrightarrow{\text{OC}} \right);\]

\[\overrightarrow{C_{1}M} = \frac{1}{3}\left( - \overrightarrow{z} + \overrightarrow{C_{1}A} + \overrightarrow{C_{1}B} \right);\ \ \]

\[\overrightarrow{B_{1}M} = \frac{1}{3}\left( - \overrightarrow{y} + \overrightarrow{B_{1}C} + \overrightarrow{B_{1}A} \right);\]

\[\overrightarrow{A_{1}M} = \frac{1}{3}\left( - \overrightarrow{x} + \overrightarrow{A_{1}B} + \overrightarrow{A_{1}C} \right).\]

\[3)\ \overrightarrow{A_{1}M} + \overrightarrow{B_{1}M} + \overrightarrow{C_{1}M} =\]

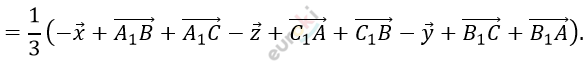
\[4)\ \overrightarrow{A_{1}M} + \overrightarrow{B_{1}M} + \overrightarrow{C_{1}M} = \overrightarrow{0}\ \ (как\ \]

\[векторы\ с\ началом\ в\ вершинах\ \]

\[треугольника\ \ и\ концом\ в\ \]

\[точке\ пересечения\ медиан):\]

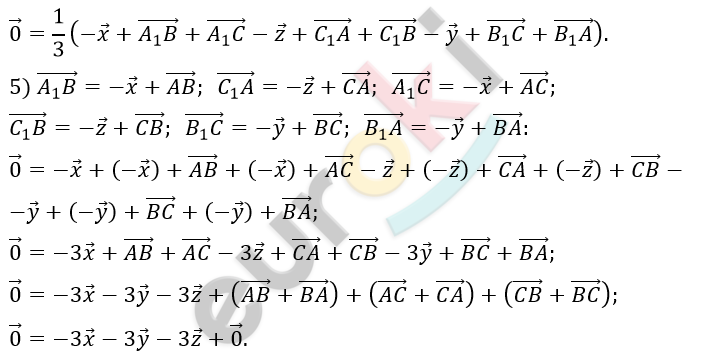
\[6)\ Таким\ образом:\]

\[\overrightarrow{x} + \overrightarrow{y} + \overrightarrow{z} = \overrightarrow{0}\ \]

\[\overrightarrow{z} = - 1\overrightarrow{x} - 1\overrightarrow{y}.\]

\[Следовательно,\ векторы\ \overrightarrow{AA_{1}},\ \]

\[\overrightarrow{BB_{1}}\ и\ \overrightarrow{CC_{1}}\ компланарны,\]

\[прямые,\ на\ которых\ они\ лежат\ \]

\[параллельны\ некоторой\ \]

\[плосоксти.\]

\[Что\ и\ требовалось\ доказать.\]