Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 10 класс Атанасян ФГОС 597
597
\[\boxed{\mathbf{597.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]
\[\textbf{а)}\ Результирующая\ \]
\[напряженность\ поля\ в\ точке\ A:\]
\[\overrightarrow{E} =\]
\[= \frac{\text{kq}}{A_{1}A^{3}} \bullet \overrightarrow{A_{1}A} + \frac{\text{kq}}{BA^{3}} \bullet \overrightarrow{\text{BA}} + \frac{\text{kq}}{DA^{3}} \bullet \overrightarrow{\text{DA}} =\]
\[= \frac{\text{kq}}{a^{3}} \bullet \left( \overrightarrow{A_{1}A} + \overrightarrow{\text{BA}} + \overrightarrow{\text{DA}} \right).\]
\[По\ правилу\ параллелепипеда:\]
\[\overrightarrow{A_{1}A} + \overrightarrow{\text{BA}} + \overrightarrow{\text{DA}} =\]
\[= - \overrightarrow{AA_{1}} - \overrightarrow{\text{AB}} - \overrightarrow{\text{AD}} = - \overrightarrow{AC_{1}};\]
\[\overrightarrow{E} = - \frac{\text{kq}}{a^{3}}\overrightarrow{AC_{1}}.\]
\[Результирующая\ \]
\[напряженность\ поля\ в\ точке\ C_{1}:\]
\[A_{1}C_{1} = BC_{1} = DC_{1} = a\sqrt{2}\ \]
\[(как\ дигонали\ квадрата):\ \]
\[A_{1}C_{1}^{3} = 2\sqrt{2} \bullet a^{3}.\]
\[По\ правилу\ параллелепипеда:\ \ \]
\[\overrightarrow{E} =\]
\[= \frac{\text{kq}}{2\sqrt{2}a^{3}} \bullet \left( \overrightarrow{A_{1}C_{1}} + \overrightarrow{BC_{1}} + \overrightarrow{DC_{1}} \right) =\]
\[= \frac{\text{kq}}{2\sqrt{2}a^{3}} \bullet 2\left( \overrightarrow{\text{AD}} + \overrightarrow{AA_{1}} + \overrightarrow{\text{AB}} \right) =\]
\[= \frac{\sqrt{2}\text{kq}}{2a^{3}} \bullet \overrightarrow{AC_{1}}.\]
\[Ответ:\ - \frac{\text{kq}}{a^{3}}\overrightarrow{AC_{1}};\ \ \ \ \frac{\sqrt{2}\text{kq}}{2a^{3}}\overrightarrow{AC_{1}}.\]
\[\textbf{б)}\ Результирующая\ \]
\[напряженность\ поля\ в\ точке\ C:\]
\[\overrightarrow{E} =\]
\[= \frac{\text{kq}}{A_{1}C} \bullet \overrightarrow{A_{1}C} + \frac{\text{kq}}{a^{3}} \bullet \overrightarrow{\text{BC}} + \frac{\text{kq}}{a^{3}} \bullet \overrightarrow{\text{DC}}.\]
\[A_{1}C = \sqrt{A_{1}A^{2} + AC^{2}} =\]
\[= \sqrt{a^{2} + a^{2} \bullet 2} = \sqrt{3a^{2}} = a\sqrt{3}:\]
\[\overrightarrow{E} - диагональ\ \]
\[параллелепипеда\ со\ сторонами\]
\[\frac{\text{kq}}{a^{3}}\frac{\sqrt{3}}{9}\overrightarrow{A_{1}C}.\]
\[По\ правилу\ параллелепипеда:\]
\[\frac{\text{kq}}{a^{3}}\left( 1 + \frac{\sqrt{3}}{9} \right)\overrightarrow{\text{BC}};\]
\[\ \frac{\text{kq}}{a^{3}}\left( 1 + \frac{\sqrt{3}}{9} \right)\overrightarrow{\text{DC}}.\]
\[Модуль\ равен:\]
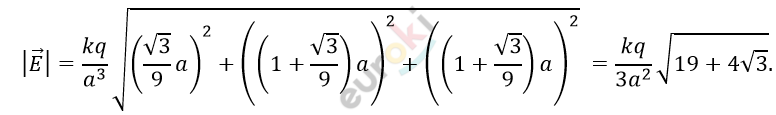
\[Результирующая\ \]
\[напряженность\ поля\ в\ точке\ \]
\[B:\]
\[\overrightarrow{E} =\]
\[= \frac{\text{kq}}{DB_{1}} \bullet \overrightarrow{DB_{1}} + \frac{\text{kq}}{a^{3}} \bullet \overrightarrow{BB_{1}} + \frac{\text{kq}}{a^{3}} \bullet \overrightarrow{A_{1}B_{1}}.\]
\[DB_{1} = A_{1}C:\ \]
\[\overrightarrow{E} = \frac{\text{kq}}{{3a}^{2}}\sqrt{19 + 4\sqrt{3}}\text{.\ }\]
\[Результирующая\ \]
\[напряженность\ поля\ в\ точке\ O:\]
\[\overrightarrow{E} =\]
\[= \frac{\text{kq}}{A_{1}O} \bullet \overrightarrow{A_{1}O} + \frac{\text{kq}}{\text{DO}} \bullet \overrightarrow{\text{DO}} + \frac{\text{kq}}{\text{BO}} \bullet \overrightarrow{\text{BO}}.\]
\[BO = DO = A_{1}O =\]
\[= \sqrt{\left( \frac{1}{2} \bullet a\sqrt{2} \right)^{2} + \left( \frac{1}{2}a \right)^{2}} = a\sqrt{\frac{3}{4}}\ :\]
\[\overrightarrow{E} = \frac{4\sqrt{4}\text{kq}}{3\sqrt{3}a^{3}}\left( \overrightarrow{\text{BO}} + \overrightarrow{\text{DO}} + \overrightarrow{A_{1}O} \right).\]
\[По\ правилу\ параллелограмма:\]
\[\overrightarrow{\text{BO}} + \overrightarrow{\text{DO}} = 2\overrightarrow{OO_{1}} = \overrightarrow{AA_{1}};\]
\[\overrightarrow{AA_{1}} + \overrightarrow{A_{1}O} = \overrightarrow{\text{AO}};\ \]
\[\left| \overrightarrow{\text{AO}} \right| = A_{1}O = a\sqrt{\frac{3}{4}}.\]
\[Таким\ образом:\ \]
\[\overrightarrow{E} = \frac{4\sqrt{4}\text{kq}}{3\sqrt{3}a^{3}} \bullet a\sqrt{\frac{3}{4}} = \frac{4kq}{3a^{2}}.\]
\[Ответ:\ \ \frac{\text{kq}}{3a^{2}}\sqrt{19 + 4\sqrt{3}};\ \ \ \]
\[\frac{\text{kq}}{3a^{2}}\sqrt{19 + 4\sqrt{3}};\ \ \ \frac{2kq}{9a^{2}}\sqrt{105}\ ;\ \ \ \ \]
\[\frac{4kq}{3a^{2}}.\]
