Решебник по геометрии 10 класс Атанасян ФГОС 587

\[\boxed{\mathbf{587.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[векторы\ \overrightarrow{a},\overrightarrow{b},\overrightarrow{c},\overrightarrow{p};\ \ \]

\[\overrightarrow{p} = \overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c};\ \ \]

\[\overrightarrow{a},\overrightarrow{b},\overrightarrow{c} - попарно\ не\ \]

\[сонаправлены.\]

\[Доказать:\]

\[\left| \overrightarrow{p} \right| < \left| \overrightarrow{a} \right| + \left| \overrightarrow{b} \right| + \left| \overrightarrow{c} \right|.\]

\[Доказательство.\]

\[1)\ \overrightarrow{p} = \overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}:\ \]

\[значит,\ векторы\ \mathbf{можно\ }\]

\[\mathbf{переместить\ так,\ чтобы\ начало\ }\]

\[\mathbf{одного\ вектора\ совпадало\ с\ }\]

\[\mathbf{концом\ другого}\mathbf{.}\]

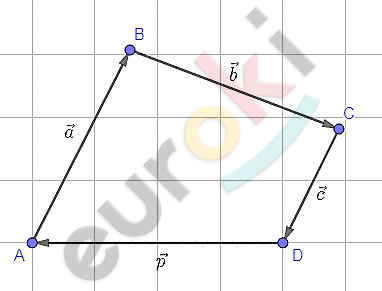
\[2)\ Пусть\ \overrightarrow{\text{AB}} = \overrightarrow{a},\ отложим:\ \ \]

\[от\ точки\ B - вектор\ \overrightarrow{\text{BC}} = \overrightarrow{b};\ \]

\[от\ точки\ C - вектор\ \overrightarrow{\text{CD}} = \overrightarrow{c}.\]

\[Получим:\ \]

\[\overrightarrow{\text{DA}} = \overrightarrow{p}.\]

\[3)\ Векторы\ \overrightarrow{a},\overrightarrow{b}\ и\ \overrightarrow{c}\ попарно\ не\ \]

\[сонаправлены:\]

\[точки\ A,B,C\ и\ D\ не\ лежат\ на\ \]

\[одной\ прямой.\ \]

\[Значит:\ \]

\[ABCD - четырехугольник.\]

\[4)\ Из\ неравенства\ \]

\[многоугольника:\text{\ \ }\]

\[AD < AB + BC + CD.\]

\[Следовательно:\]

\[\left| \overrightarrow{p} \right| < \left| \overrightarrow{a} \right| + \left| \overrightarrow{b} \right| + \left| \overrightarrow{c} \right|.\]

\[Что\ и\ требовалось\ доказать.\]