Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 10 класс Атанасян ФГОС 548
548
\[\boxed{\mathbf{548.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]
\[Дано:\]
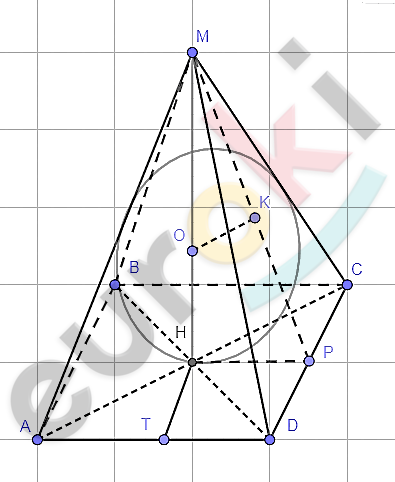
\[MABCD - пирамида;\]
\[ABCD - ромб;\]
\[\angle DAC = \alpha;\]
\[AB = a;\]
\[\angle MPH = \beta;\]
\[O - центр\ вписанного\ шара.\]
\[Найти:\]
\[V_{шара}.\]
\[Решение.\]
\[1)\ MH - высота\ пирамиды.\]
\[2)\ Построим\ HP\bot DC\ \ и\ \ \]
\[HT\bot AD:\]
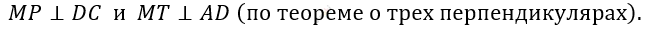
\[\angle MTH = \angle MPH = \beta - как\ \]
\[линейный\ угол\ двугранного\ \]
\[угла\ между\ боковыми\ гранями\ \]
\[и\ основанием\ пирамиды\ \]
\[\text{MABCD.}\]
\[3)\ \mathrm{\Delta}MHT = \mathrm{\Delta}MHP:\ \]
\[MH - общий\ катет;\]
\[\angle MTH = \angle MPH.\]
\[Отсюда:\]
\[HT = HP = r - радиус\ \]
\[вписанной\ в\ \text{ABCD\ }окружности\ \]
\[с\ центром\ \ \]
\[в\ точке\ \text{H.}\]
\[4)\ Площадь\ основания\ \]
\[пирамиды:\]
\[S_{\text{ABCD}} = 2 \bullet \frac{1}{2} \bullet a \bullet a \bullet \sin\alpha =\]
\[= a^{2} \bullet \sin\alpha = 4 \bullet S_{\text{HCD}} =\]
\[= 4 \bullet \frac{1}{2} \bullet a \bullet HP = 2a \bullet HP;\]
\[a^{2} \bullet \sin\alpha = 2a \bullet HP\]
\[HP = \frac{a \bullet \sin\alpha}{2}.\]
\[5)\ В\ \mathrm{\Delta}MPH:\ \ \]
\[PO - биссектриса\ угла\ \beta;\]
\[\angle HPO = \angle OPM = \frac{\beta}{2}.\]
\[6)\ \mathrm{\Delta}HPO - прямоугольный:\]
\[\frac{\text{OH}}{\text{HP}} = tg\frac{\beta}{2}\]
\[OH = R = HP \bullet tg\frac{\beta}{2} =\]
\[= \frac{a \bullet \sin\alpha \bullet tg\frac{\beta}{2}}{2}.\]
\[7)\ V_{шара} = \frac{4}{3}\pi \bullet R^{3} =\]
\[= \frac{4}{3}\pi \bullet \left( \frac{a \bullet \sin\alpha \bullet tg\frac{\beta}{2}}{2} \right)^{3} =\]
\[= \frac{\pi}{6}a^{3} \bullet \sin^{3}\alpha \bullet tg^{3}\frac{\beta}{2}.\]
\[\mathbf{Отв}ет:\ \ \frac{\pi}{6}a^{3} \bullet \sin^{3}\alpha \bullet tg^{3}\frac{\beta}{2}.\]
