Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по геометрии 10 класс Атанасян ФГОС 541
541
\[\boxed{\mathbf{541.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]
\[Дано:\]
\[конус;\]
\[MABCD - вписанная\ пирамида;\]
\[AB > AD = a;\]
\[\angle MPH = \varphi_{2};\]
\[\angle BHC = \varphi_{1}.\]
\[Найти:\]
\[\text{V.}\]
\[Решение.\]
\[1)\ В\ плоскости\ \text{ABCD\ }построим\ \]
\[HP\bot AD:\]
\[MP\bot AD\ \]
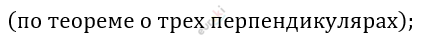
\[\angle MPH = \varphi_{2} - линейный\ угол\ \]
\[двугранного\ угла\ межу\ \]
\[боковой\ гранью\ с\ меньшей\ \]
\[стороной\ прямоугольника\ \]
\[\text{ABCD\ }и\ плоскостью\ \]
\[основания\ пирамиды.\]
\[\frac{\text{MH}}{\text{HP}} = tg\ \varphi_{2}\]
\[MH = HP \bullet tg\ \varphi_{2}.\]
\[2)\ В\ прямоугольнике\ ABCD:\ \ \]
\[AH = HC = HB = HD.\]
\[3)\ \angle BHC = \angle AHD =\]
\[= \frac{180{^\circ} - \varphi_{1}}{2} = 90{^\circ}\ - \frac{\varphi_{1}}{2}.\]
\[4)\ По\ теореме\ синусов\ в\ \mathrm{\Delta}\text{ADH\ }\]
\[(AH = DH):\]
\[\frac{a}{\sin\varphi_{1}} = \frac{\text{AH}}{\sin\left( 90{^\circ} - \frac{\varphi_{1}}{2} \right)}\]
\[AH = \frac{a \bullet \sin\left( 90{^\circ} - \frac{\varphi_{1}}{2} \right)}{\sin\varphi_{1}}\]
\[AH = \frac{a \bullet \cos\frac{\varphi_{1}}{2}}{2 \bullet \sin\frac{\varphi_{1}}{2} \bullet \cos\frac{\varphi_{1}}{2}} =\]
\[= \frac{a}{2 \bullet \sin\frac{\varphi_{1}}{2}}.\]
\[5)\ В\ \mathrm{\Delta}AHP:\ \ \]
\[HP = AH \bullet \cos\frac{\varphi_{1}}{2} =\]
\[= \frac{a}{2 \bullet \sin\frac{\varphi_{1}}{2}} \bullet \cos\frac{\varphi_{1}}{2} = \frac{a}{2 \bullet tg\frac{\varphi_{1}}{2}};\]
\[MH = HP \bullet tg\ \varphi_{2} = \frac{a \bullet tg\ \varphi_{2}}{2 \bullet tg\frac{\varphi_{1}}{2}}.\]
\[6)\ V = \frac{1}{3}\pi r^{2}h = \frac{1}{3}\pi \bullet AH \bullet MH;\]
\[V = \frac{1}{3}\pi \bullet \frac{a^{2}}{4 \bullet \sin^{2}\frac{\varphi_{1}}{2}} \bullet \frac{a \bullet tg\ \varphi_{2}}{2\ tg\frac{\varphi_{1}}{2}} =\]
\[= \frac{\pi a^{3} \bullet tg\ \varphi_{2}}{{24 \bullet \sin^{2}}\frac{\varphi_{1}}{2} \bullet tg\frac{\varphi_{1}}{2}}.\]
\[\mathbf{Отв}ет:\ \ V = \frac{\pi a^{3} \bullet tg\ \varphi_{2}}{{24 \bullet \sin^{2}}\frac{\varphi_{1}}{2} \bullet tg\frac{\varphi_{1}}{2}}.\]
