Решебник по геометрии 10 класс Атанасян ФГОС 534

\[\boxed{\mathbf{534.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

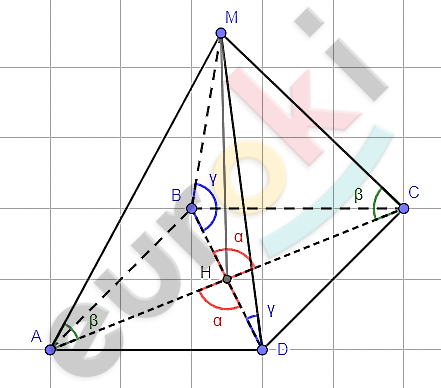
\[MABCD - пирамида;\]

\[MH = h;\]

\[\angle AHD = \alpha;\]

\[\angle BHC = \alpha;\]

\[\angle MAC = \beta;\]

\[\angle MCA = \beta;\]

\[\angle MBD = \gamma;\]

\[MDB = \gamma.\]

\[Найти:\]

\[\text{V.}\]

\[Решение.\]

\[1)\ \mathrm{\Delta}MHB - прямоугольный:\ \]

\[\frac{\text{MH}}{\text{HB}} = tg\ \gamma;\ \ \frac{h}{\text{HB}} = tg\ \gamma;\ \]

\[HB = \frac{h}{\text{tg\ γ}}.\]

\[2)\ \mathrm{\Delta}MAH - прямоугольный:\]

\[\frac{\text{MH}}{\text{HA}} = tg\ \beta;\ \ \ \frac{h}{\text{HA}} = tg\ \beta;\]

\[HA = \frac{h}{\text{tg\ β}}.\]

\[3)\ HA = \frac{1}{2}AC \rightarrow AC = \frac{2h}{\text{tg\ β}};\]

\[HB = \frac{1}{2}BD \rightarrow \ BD = \frac{2h}{\text{tg\ γ}}.\]

\[4)\ Площадь\ основания\ \]

\[пирамиды:\]

\[S_{осн} = S_{\text{ABCD}} =\]

\[= \frac{1}{2}AC \bullet BD \bullet \sin\alpha =\]

\[= \frac{1}{2} \bullet \frac{2h}{\text{tg\ β}} \bullet \frac{2h}{\text{tg\ γ}} \bullet \sin a =\]

\[= \frac{2h^{2} \bullet \sin\alpha}{tg\ \beta \bullet tg\ \gamma}.\]

\[5)\ V = \frac{1}{3} \bullet S_{осн} \bullet h =\]

\[= \frac{1}{3} \bullet \frac{2h^{2} \bullet \sin\alpha}{tg\ \beta \bullet tg\ \gamma} \bullet h =\]

\[= \frac{2h^{3} \bullet \sin\alpha}{3 \bullet tg\ \beta \bullet tg\ \gamma}.\]

\[\mathbf{Отв}ет:\ \ V = \frac{2h^{3} \bullet \sin\alpha}{3 \bullet tg\ \beta \bullet tg\ \gamma}.\]