Решебник по геометрии 10 класс Атанасян ФГОС 347

\[\boxed{\mathbf{347.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

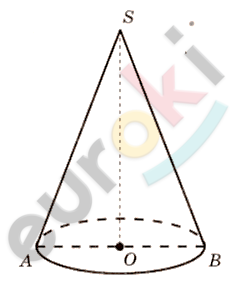
\[l = AS = 12\ см.\]

\[Найти:\]

\[S_{осн}.\]

\[Решение.\]

\[R = OA = AS \cdot \cos\alpha;\]

\[S_{осн} = \pi R^{2}.\]

\[\textbf{а)}\ \alpha = 30{^\circ}:\]

\[R = 12 \cdot \frac{\sqrt{3}}{3} = 6\sqrt{3}\ см.\]

\[S_{осн} = \pi \cdot \left( 6\sqrt{3} \right)^{2} = 108\pi\ \left( см^{2} \right).\]

\[\textbf{б)}\ \alpha = 45{^\circ}:\]

\[R = 12 \cdot \frac{\sqrt{2}}{2} = 6\sqrt{2}\ см.\]

\[S_{осн} = \pi \cdot \left( 6\sqrt{2} \right)^{2} = 72\pi\ \left( см^{2} \right).\]

\[\textbf{в)}\ \alpha = 60{^\circ}:\]

\[R = 12 \cdot \frac{1}{2} = 6\ см.\]

\[S_{осн} = \pi \cdot 6^{2} = 36\pi\ \left( см^{2} \right).\]