Решебник по геометрии 10 класс Атанасян ФГОС 31

\[\boxed{\mathbf{31.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

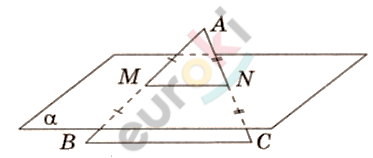
\[⊿ABC;\]

\[BC \parallel \alpha;\]

\[AM = MB;\]

\[MN \parallel \alpha.\]

\[Доказать:\]

\[AN = NC.\]

\[Доказательство.\]

\[1)\ Если\ плоскость\ \text{ABC\ }\]

\[проходит\ через\ данную\ \]

\[прямую\ \text{AB},\ параллельную\ \]

\[другой\ плоскости\ \alpha\ и\ \]

\[пересекающую\ эту\ плоскость,\]

\[то\ линия\ пересечения\ \]

\[плоскостей\ MN \parallel BC.\]

\[2)\ В\ плоскости\ \text{ABC}\ прямая,\ \]

\[проходящая\ через\ середину\ \]

\[стороны\ \text{AB},параллельно\ \]

\[основанию\ \text{BC},\ проходит\ и\ \]

\[через\ середину\ второй\]

\[стороны\ \text{AC},\ то\ есть\ содержит\ \]

\[среднюю\ линию.\]

\[3)\ Следовательно:\]

\[AN = NC.\]

\[Что\ и\ требовалось\ доказать.\]