Решебник по геометрии 10 класс Атанасян ФГОС 308

\[\boxed{\mathbf{308.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

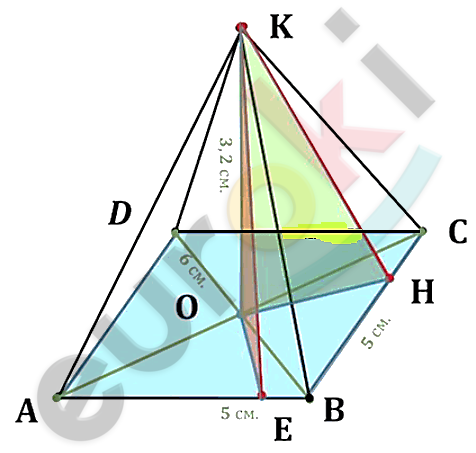
\[ABCD - ромб;\]

\[AB = 5\ см;\]

\[BD = 6\ см;\]

\[O - точка\ пересечения\ \]

\[диагоналей\ ромба;\]

\[OK\bot ABCD;\]

\[OK = 3,2\ см;\]

\[KE\bot AB;\]

\[KH\bot BC.\]

\[Найти:\]

\[высоты\ боковых\ граней.\]

\[Решение.\ \]

\[По\ свойству\ ромба:\]

\[\angle AOB = 90{^\circ};\]

\[DO = OB = \frac{\text{BD}}{2} = 3\ см.\]

\[⊿AOB = ⊿BOC = ⊿COD =\]

\[= ⊿DOA - по\ построению\ \]

\[(прямоугольные):\]

\[высоты,\ проведенные\ к\ \]

\[основанию,\ равны;\]

\[боковые\ грани\ равны.\]

\[Найдем\ высоту\ \text{KH.}\]

\[По\ теореме\ Пифагора\ \]

\[(из\ ⊿AOB):\]

\[AO = \sqrt{AB^{2} - OB^{2}} = \sqrt{25 - 9} =\]

\[= 4\ см.\]

\[OH - высота,\ проведенная\ к\ \]

\[гипотенузе:\]

\[OH = h = \frac{a \cdot b}{c} = \frac{OB \cdot OC}{\text{BC}} =\]

\[= \frac{3 \cdot 4}{5} = 2,4\ см.\]

\[По\ теореме\ Пифагора\ \]

\[(из\ ⊿HOK):\]

\[KH = \sqrt{OK^{2} + HO^{2}} =\]

\[= \sqrt{{3,2}^{2} + {2,4}^{2}} = \sqrt{16} = 4\ см.\]

\[Ответ:все\ высоты\ равны\ 4\ см.\]