Решебник по геометрии 10 класс Атанасян ФГОС 270

\[\boxed{\mathbf{270.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

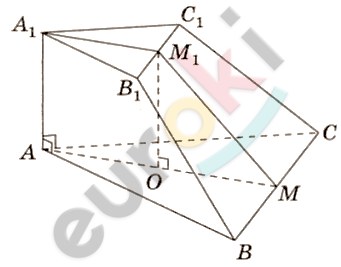
\[Найти:\]

\[S_{бок}.\]

\[Решение.\]

\[1)\ AM\bot BC;\ \ A_{1}M_{1}\bot B_{1}C_{1}:\]

\[M_{1}M\bot BC - по\ теореме\ о\ трех\ \]

\[перпендикулярах;\]

\[MM_{1} - высота\ боковой\ грани;\]

\[M_{1}O\bot\text{AM.}\]

\[2)\ По\ определению\ синуса\ \]

\[\left( из\ ⊿A_{1}M_{1}B_{1} \right):\]

\[A_{1}M_{1} = A_{1}B_{1} \cdot \sin{60{^\circ}} = \frac{3\sqrt{3}}{2}\ см.\]

\[3)\ По\ определению\ синуса\ \]

\[(из\ ⊿AMB):\]

\[AM = AB \cdot \sin{60{^\circ}} = \frac{5\sqrt{3}}{2}\ см;\]

\[OM = AM - AO = AM - A_{1}M_{1} =\]

\[= \frac{5\sqrt{3}}{2} - \frac{3\sqrt{3}}{2} = \frac{2\sqrt{3}}{2} = \sqrt{3}\ см.\]

\[4)\ По\ теореме\ Пифагора\ \]

\[\left( из\ ⊿M_{1}OM;\ \angle O = 90{^\circ} \right):\]

\[MM_{1} = \sqrt{M_{1}O^{2} + OM^{2}} =\]

\[= \sqrt{1^{2} + \left( \sqrt{3} \right)^{2}} = 2\ см.\]

\[5)\ S_{B_{1}C_{1}\text{CB}} = \frac{B_{1}C_{1} + BC}{2} \cdot MM_{1} =\]

\[= \frac{3 + 5}{2} \cdot 2 = 8\ см^{2};\]

\[S_{AA_{1}B_{1}B} = \frac{3 + 5}{2} \cdot 1 = 4\ см^{2};\]

\[S_{AA_{1}C_{1}C} = S_{AA_{1}B_{1}B} = 4\ см^{2};\]

\[S_{бок} =\]

\[= S_{B_{1}C_{1}\text{CB}} + S_{AA_{1}B_{1}B} + S_{AA_{1}C_{1}C} =\]

\[= 8 + 4 + 4 = 16\ см^{2}.\]

\[Ответ:16\ см^{2}.\]

\[Параграф\ 3.\ Правильные\ многогранники\]