Решебник по геометрии 10 класс Атанасян ФГОС 265

\[\boxed{\mathbf{265.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

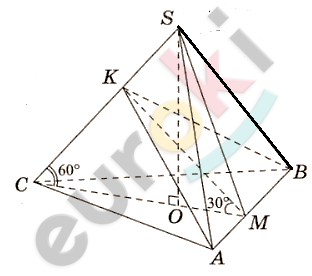
\[SO - высота;\]

\[O - центр\ ⊿ABC;\]

\[AB = BC = AC = 12\ см.\]

\[Найти:\]

\[S_{сеч}.\]

\[Решение.\]

\[CM\bot AB;\ \ SM\bot AB:\]

\[CMS\bot AB - по\ теореме\ о\ трех\ \]

\[перпендикулярах.\]

\[KM\bot AB;CM\bot AB:\]

\[\angle CMK = 30{^\circ} - линейный\ угол\ \]

\[двугранного\ угла\ при\ \]

\[основании\ пирамиды,\ \]

\[образованный\ плоскоскостью\ \]

\[пересечения\ с\ основанием.\]

\[В\ треугольнике\ SOC:\]

\[CO - проекция\ ребра\ \text{CS.}\]

\[В\ правильной\ пирамиде\ все\ \]

\[боковые\ ребра\ одинаковы\ и\ \]

\[наклонены\ к\ основанию\ под\ \]

\[одинаковым\ углом:\]

\[\angle SCO = 60{^\circ}.\]

\[В\ треугольнике\ AKB:\]

\[S_{\text{AKB}} = \frac{1}{2}KM \cdot AB = \frac{1}{2}KM \cdot 12 =\]

\[= 6KM.\]

\[По\ определению\ синуса\ \]

\[(в\ ⊿AMC):\]

\[MC = AC \cdot \sin{\angle CAB} = 12 \cdot \frac{\sqrt{3}}{2} =\]

\[= 6\sqrt{3}\ см.\]

\[По\ определению\ синуса\ \]

\[(в\ ⊿MKC):\]

\[MK = MC \cdot \sin{\angle SCO} =\]

\[= \frac{6\sqrt{3} \cdot \sqrt{3}}{2} = 9\ см.\]

\[S_{\text{AKB}} = 6MK = 6 \cdot 9 = 54\ см^{2}.\]

\[Ответ:54\ см^{2}.\]