Решебник по геометрии 10 класс Атанасян ФГОС 255

\[\boxed{\mathbf{255.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

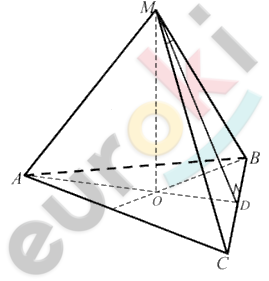
\[AB = 8\ см;\]

\[\angle CMB = \varphi.\]

\[Найти:\]

\[\text{MO.}\]

\[Решение.\]

\[1)\ MABC - правильная\ \]

\[пирамида:\]

\[O - центр\ треугольника\ ABC;\]

\[AO = R;\]

\[OD = r;\]

\[AO = 2OD.\]

\[2)\ AO = \frac{8}{\sqrt{3}};\ \ OD = \frac{4}{\sqrt{3}}.\]

\[В\ треугольнике\ MOD:\]

\[MO^{2} = MD^{2} - OD^{2}.\]

\[3)\ ⊿CDM - прямоугольный:\]

\[CD = \frac{1}{2}BC;\]

\[\angle CMD = \frac{\varphi}{2}.\]

\[4)\ tg\frac{\varphi}{2} = \frac{\text{DC}}{\text{MD}};\]

\[MD = 4\ :tg\frac{\varphi}{2} = \frac{4}{\text{tg}\frac{\varphi}{2}};\]

\[MO = \sqrt{\left( \frac{4}{\text{tg}\frac{\varphi}{2}} \right)^{2} - \left( \frac{4}{\sqrt{3}} \right)^{2}} =\]

\[= \frac{4}{\text{tg}\frac{\varphi}{2}}\sqrt{1 - \frac{1}{3}tg^{2}\frac{\varphi}{2}}.\]

\[Ответ:\ \frac{4}{\text{tg}\frac{\varphi}{2}}\sqrt{1 - \frac{1}{3}tg^{2}\frac{\varphi}{2}}.\]