Решебник по геометрии 10 класс Атанасян ФГОС 253

\[\boxed{\mathbf{253.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[ABCD - равнобедренная\ \]

\[трапеция;\]

\[AB = CD;\]

\[AD = 4\sqrt{6}\ см;\]

\[BC = 6\ см;\]

\[CK = 5\ см - высота\ трапеции;\]

\[SO = h - высота\ пирамиды.\]

\[Найти:\]

\[\text{h.}\]

\[Решение.\]

\[1)\ Равные\ проекции\ имеют\ \]

\[равные\ наклонные:\]

\[OA = OB = OC = OD = R -\]

\[радиус\ окружности,\ описанной\ \]

\[около\ \text{ABCD.}\]

\[2)\ R = OA - в\ ⊿ACD;AC -\]

\[диагональ:\]

\[R = \frac{\text{abc}}{4S} = \frac{AC \cdot CD \cdot AD}{4S_{\text{ACD}}}.\]

\[3)\ По\ определению\ косинуса\ \]

\[\left( из\ ⊿\text{CDK} \right):\]

\[\cos{\angle CDK} = \frac{\text{KD}}{\text{CD}};\]

\[KD = \frac{AD - BC}{2} = \frac{4\sqrt{6} - 6}{2} =\]

\[= 2\sqrt{6} - 3\ (см).\]

\[4)\ По\ теореме\ Пифагора:\]

\[CD = \sqrt{CK^{2} + KD^{2}} =\]

\[= \sqrt{5^{2} + \left( 2\sqrt{6} - 3 \right)^{2}} =\]

\[= \sqrt{25 + 24 - 12\sqrt{6} + 9} =\]

\[= \sqrt{\left( 3\sqrt{6} - 2 \right)^{2}} = 3\sqrt{6} - 2\ \ (см).\]

\[\cos{\angle CDK} = \frac{2\sqrt{6} - 3}{3\sqrt{6} - 2}.\]

\[5)\ По\ теореме\ косинусов\ \]

\[\left( ⊿\text{ACD} \right):\]

\[AC^{2} =\]

\[= CD^{2} + AD^{2} - 2CD \cdot AD \cdot \cos{\angle CDA} =\]

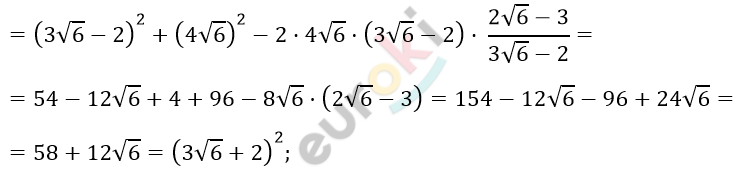
\[AC = 3\sqrt{6} + 2\ \ см.\]

\[R =\]

\[= \frac{\left( 3\sqrt{6} + 2 \right)\left( 3\sqrt{6} - 2 \right) \cdot 4\sqrt{6}}{4 \cdot \frac{1}{2} \cdot 4\sqrt{6} \cdot 5} =\]

\[= \frac{50}{10} = 5\ см.\]

\[6)\ По\ теореме\ Пифагора\ \]

\[(из\ ⊿AOS):\]

\[SO = \sqrt{AS^{2} - AO^{2}} =\]

\[= \sqrt{13^{2} - 5^{2}} = 12\ см.\]

\[Ответ:12\ см.\]