Решебник по геометрии 10 класс Атанасян ФГОС 161

\[\boxed{\mathbf{161.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[\text{BA} \in CBD;\]

\[\angle ABC < 90{^\circ};\]

\[\angle ABC = \angle ABD.\]

\[Доказать:\]

\[проекция\ BA\ на\ CBD -\]

\[биссектриса\ \angle CBD.\]

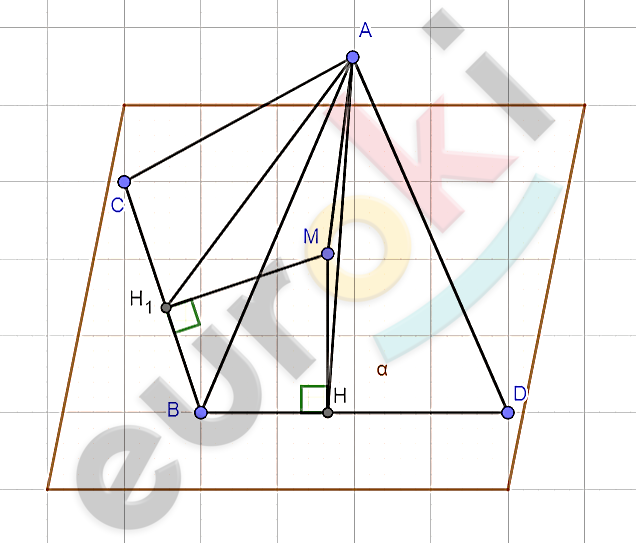
\[Доказательство.\]

\[1)\ Построим\ AM\bot\alpha.\]

\[2)\ В\ плоскости\ \alpha\ построим\ \]

\[\text{MH\ }и\ MH_{1},\ перпендикулярные\]

\[\ \text{BD\ }и\ \text{BC\ }соответственно.\]

\[3)\ HM\bot BD\ и\ H_{1}M\bot CB:\]

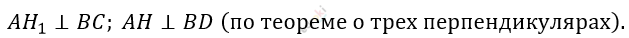
\[4)\ \mathrm{\Delta}ABH = \mathrm{\Delta}\text{AB}H_{1} - по\ \]

\[гипотенузе\ и\ острому\ углу:\]

\[\angle ABH_{1} = \angle ABH;\]

\[AB - общая\ сторона.\]

\[Отсюда:\ \]

\[BH = BH_{1}.\]

\[5)\ В\ плоскости\ \alpha\ построим\ \]

\[BM - проекцию\ \text{AB.}\]

\[6)\ \mathrm{\Delta}BMH = \mathrm{\Delta}\text{BM}H_{1} - по\ углу\ и\ \]

\[двум\ сторонам:\]

\[BM - общая;\ \]

\[BH = BH_{1}\text{.\ }\]

\[Отсюда:\ \]

\[7)\ \angle CBD = \angle MBH + \angle MBH_{1}:\ \]

\[BM - биссектрисса\ \angle DCB.\]

\[Что\ и\ требовалось\ доказать.\]