Решебник по геометрии 10 класс Атанасян ФГОС 150

\[\boxed{\mathbf{150.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

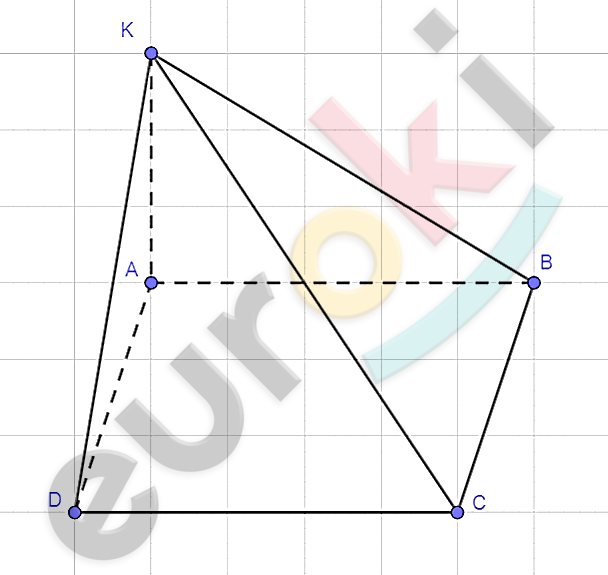
\[ABCD - прямоугольный;\]

\[AK\bot ABCD;\]

\[KD = 9\ см;\]

\[KB = 7\ см;\]

\[KC = 9\ см.\]

\[Найти:\]

\[\textbf{а)}\ p(K,ABCD);\]

\[\textbf{б)}\ p(AK,CD).\]

\[Решение.\]

\[\textbf{а)}\ p(K,ABCD) = KA:\ \]

\[KA\bot ABCD.\]

\[\mathrm{\Delta}DKC - прямоугольный:\]

\[\angle KDC = 90{^\circ}\ \]

\[(\ так\ как\ KA\bot CD,\ AD\bot CD).\]

\[DC = \sqrt{CK^{2} - DK^{2}} =\]

\[= \sqrt{81 - 36} = 3\sqrt{5}\ см.\]

\[\mathrm{\Delta}KAB - прямоугольный:\]

\[KA = \sqrt{BK^{2} - AB^{2}} =\]

\[= \sqrt{49 - 45} = 2\ см.\]

\[\textbf{б)}\ DC \parallel AB,\ AB \in ABK:\]

\[\ DC \parallel ABK;\]

\[p(AK,DC) = DA\ (DA\bot ABK).\]

\[\mathrm{\Delta}ADK - прямоугольный:\]

\[DA = \sqrt{DK^{2} - AK^{2}} = \sqrt{36 - 4} =\]

\[= 4\sqrt{2}\ см.\]

\[Ответ:а)\ p(K,ABCD) = 2\ см;\]

\[\textbf{б)}\ p(AK,CD) = 4\sqrt{2}\ см.\]