Решебник по геометрии 10 класс Атанасян ФГОС 146

\[\boxed{\mathbf{146.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[a \cap \alpha = M;\]

\[a\bot\text{α.}\]

\[Доказать:\]

\(в\ \alpha\ через\ M\) \(проходит\ \)

\[прямая\bot a,и\ притом\]

\[только\ одна.\]

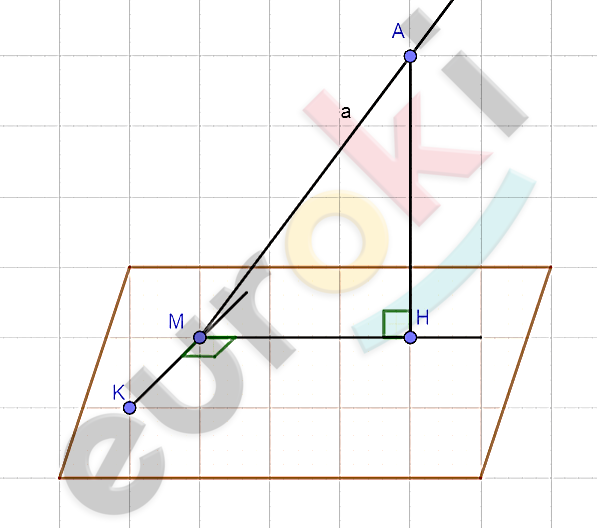
\[Доказательство.\]

\[1)\ Из\ точки\ A \in a\ опустим\ \]

\[перпендикуляр\ \text{AH\ }на\ \alpha\ (по\ \]

\[теореме\ п.18\ он\ существует,\ и\ \]

\[притом\ только\ один).\]

\[2)\ Проведем\ прямую\ \text{MH.}\]

\[3)\ В\ плоскости\ \alpha\ через\ точку\ \text{M\ }\]

\[проходит\ прямая,\ \]

\[перпендикулярная\ к\ MH\ и\ \]

\[притом\ только\ одна\ \]

\[(курс\ планиметрии).\]

\[Обозначим\ эту\ прямую\ \text{MK\ }\]

\[(MK\bot MH).\]

\[4)\ AM - наклонная,\ \]

\[MH - проекция,\ MK\bot MH:\]

\[AM\bot MK - по\ теореме\ о\ трех\ \]

\[перпендикулярах.\]

\[так\ как\ AM \in a,\ то\ и\ a\bot MK.\]

\[5)\ MK\bot MH\ и\ MK\bot AM:\]

\[MK\bot AMK.\]

\[6)\ Предположим,\ что\ в\ \]

\[плоскости\ \alpha\ существует\ еще\ \]

\[одна\ прямая\ MQ\bot a:\ \]

\[MQ\bot AMK\ \]

\[(так\ как\ MQ\bot MA;\ MQ\bot MH).\]

\[Но\ через\ точку\ \text{M\ }уже\ проходит\ \]

\[прямая\ MK\bot AMK,\]

\[а\ по\ теореме\ п.18\ такая\ прямая\ \]

\[существует\ только\ одна:\]

\[MK = MQ.\]

\[Таким\ образом,\ в\ плоскости\ \alpha\ \]

\[существует\ прямая,\ \]

\[проходящая\ через\ точку\ \text{M\ }и\ \]

\[перпендикулярная\ к\ \text{a\ }и\ \]

\[притом\ только\ одна.\]

\[Что\ и\ требовалось\ доказать.\]