Решебник по геометрии 10 класс Атанасян ФГОС 142

\[\boxed{\mathbf{142.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[\textbf{а)}\ AH = 4\ см;\]

\[BN = 1\ см;\]

\[HK = KN;\]

\[AO = OB.\]

\[\textbf{б)}\ AB \cap \alpha = M.\]

\[Найти:\]

\[\text{OK.}\]

\[Решение.\]

\[\textbf{а)}\]

\[1)\ AH\bot\alpha\ и\ BN\bot\alpha:\ \]

\[AH \parallel BN;\]

\[ABNH - трапеция.\]

\[2)\ OK\bot\alpha\ и\ AH\bot\alpha:\ \]

\[OK \parallel AH \parallel BN;\]

\[O - середина\ AB;\ \]

\[OK - средняя\ линия\ трапеции\ \]

\[\text{ABNH.}\]

\[Отсюда:\ \]

\[OK = \frac{1}{2}(AH + BN) = \frac{4 + 1}{2} =\]

\[= 2,5\ см.\]

\[\textbf{б)}\ \]

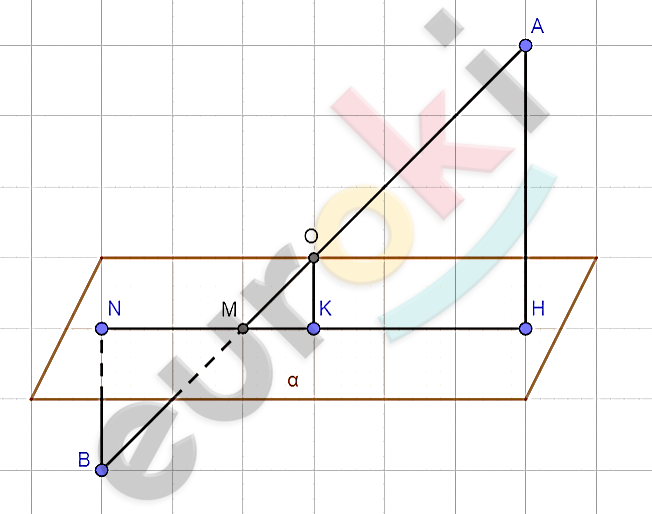
\[1)\ \mathrm{\Delta}AMH\sim\mathrm{\Delta}BMN - по\ двум\ \]

\[углам:\]

\[AH \parallel BN;\ \]

\[\angle AMH = \angle BMN\ \]

\[(как\ вертикальные);\ \]

\[Отсюда:\ \]

\[BM\ :AM = BN\ :AH = 1\ :4;\]

\[AB\ :BM = 5\ :1\]

\[AB = 5BM.\]

\[2)\ \mathrm{\Delta}OMK\sim\mathrm{\Delta}BMN - по\ двум\ \]

\[углам:\]

\[OK \parallel BN;\ \]

\[\angle OMK = \angle BMN\ \]

\[(как\ вертикальные);\ \]

\[Отсюда:\ \]

\[OK\ :BN = OM\ :BM.\]

\[3)\ BO = \frac{5}{2}\text{BM}\]

\[OM = BO - BM = \frac{5}{2}BM - BM =\]

\[= \frac{3}{2}\text{BM}\]

\[OK\ :BN = \frac{3}{2}BM\ :BM = \frac{3}{2}\]

\[OK\ :1 = \frac{3}{2} = 1,5\ см.\]

\[Ответ:а)\ 3\ см;б)\ 1,5\ см.\]