Решебник по геометрии 10 класс Атанасян ФГОС 112

\[\boxed{\mathbf{112.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[\text{ABCD}A_{1}B_{1}C_{1}D_{1} -\]

\[параллелепипед.\]

\[Доказать:\]

\[A_{1}C^{2} + B_{1}D^{2} + C_{1}A^{2} + BD^{2} =\]

\[= 4AB^{2} + 4AD^{2} + 4A_{1}A^{2}.\]

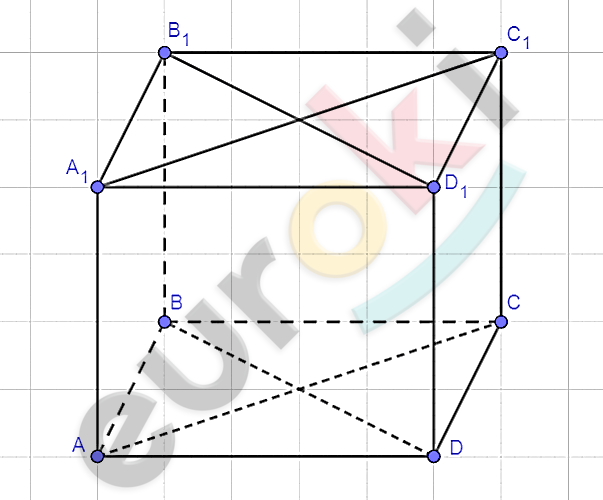
\[Доказательство.\]

\[1)\ ABCDA_{1}B_{1}C_{1}D_{1} -\]

\[параллелепипед:\]

\[ABCD - параллелограмм.\]

\[2)\ Рассмотрим\ \]

\[параллелограмм\ ABCD:\]

\[\angle ADC = 180{^\circ} - \angle DAB.\]

\[3)\ Рассмотрим\ \mathrm{\Delta}\text{ABD\ }\]

\[(по\ теореме\ косинусов):\]

\[DB^{2} =\]

\[= AD^{2} + DC^{2} - 2AD \bullet DC \bullet \cos{\angle DAB}.\]

\[4)\ Рассмотрим\ \mathrm{\Delta}\text{ACD\ }\]

\[(по\ теореме\ косинусов):\]

\[5)\ Рассмотрим\ DD_{1}B_{1}B:\]

\[D_{1}B^{2} + B_{1}D^{2} = 2DB^{2} + 2B_{1}B^{2}.\]

\[6)\ Рассмотрим\ AA_{1}CC_{1}:\]

\[A_{1}C^{2} + C_{1}A^{2} = 2AC^{2} + 2A_{1}A^{2}.\]

\[7)\ Сумма\ всех\ ребер\ \]

\[параллелепипеда:\]

\[2BD^{2} + 2B_{1}B^{2} + 2AC^{2} + 2A_{1}A^{2} =\]

\[= 2\left( DB^{2} + AC^{2} \right) + 2A_{1}A^{2} + 2A_{1}A^{2} =\]

\[= 4DA^{2} + 4A_{1}A^{2} + 4AB^{2}.\]

\[Что\ и\ требовалось\ доказать.\]