Решебник по геометрии 10 класс Атанасян ФГОС 108

\[\boxed{\mathbf{108.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[DABC - тетраэдр;\]

\[A_{1} \in BC;\]

\[B_{1} \in CA;\]

\[C_{1} \in AB.\]

\[Доказать:\]

\[AA_{1} \cap BB_{1} \cap CC_{1} = Z_{1}.\]

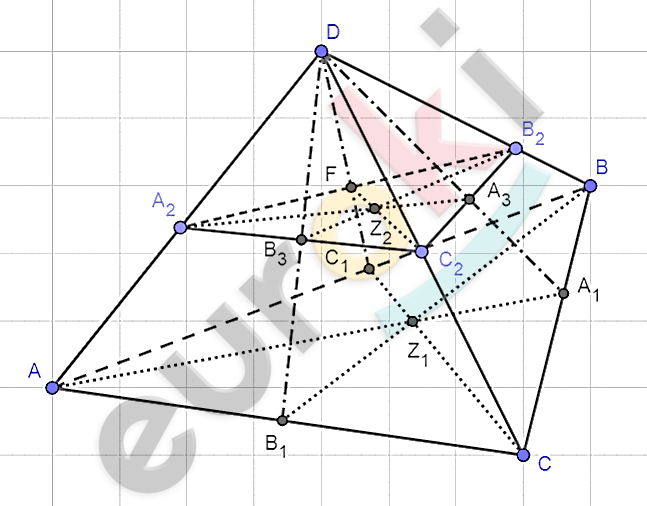
\[Доказательство.\]

\[1)\ Построим\ на\ BD,CD\ и\ \text{AD\ }\]

\[точки\ A_{2},B_{2}\ и\ C_{2}\ так,\ чтобы:\]

\[DA_{2} = DB_{2} = DC_{2}.\]

\[2)\ Отметим\ точки:\]

\[DC_{1} \cap A_{2}B_{2} = F;\]

\[DA_{1} \cap B_{2}C_{2} = A_{3};\]

\[DB_{1} \cap A_{2}C_{2} = B_{3}.\]

\[3)\ \mathrm{\Delta}A_{2}B_{2}D - равнобедренный:\]

\[A_{2}D = B_{2}\text{D.}\]

\[DF - биссектрисса\ и\ медиана:\]

\[A_{2}C_{2} = FB_{2};\ \]

\[A_{3}B_{2} = A_{3}C_{2};\]

\[B_{3}C_{2} = B_{3}A_{2}.\]

\[Отсюда:\]

\[A_{2}A_{3};\ B_{2}B_{3};\ C_{2}F - медианы\ \]

\[\mathrm{\Delta}A_{2}B_{2}C_{2}\ пересекаются\ в\ \]

\[точке\ Z_{2}\text{.\ }\]

\[4)\ Значит:\ \]

\[плоскости\ A_{2}DZ_{2},\ B_{2}DZ_{2}\ и\ \]

\[C_{2}DZ_{2}\ пересекаются\ по\ оси\ DZ_{2}.\]

\[5)\ DAA_{1} \cap DCC_{1} \cap DBB_{1} = DZ_{2}:\]

\[AA_{1} \cap BB_{1} \cap CC_{1} = Z_{1} \in DZ_{2}.\]

\[Что\ и\ требовалось\ доказать.\]