Решебник по геометрии 10 класс Атанасян ФГОС 101

\[\boxed{\mathbf{101.}ОК\ ГДЗ\ –\ домашка\ на\ 5}\]

\[Дано:\]

\[DABC - тетраэдр;\]

\[M,N,P,Q,L,K - середины\ \]

\[ребер.\]

\[Доказать:\]

\[отрезки,\ соединяющие\ \]

\[середины\ сторон,\ делятся\ \]

\[точкой\ пересечения\ пополам.\]

\[Доказательство.\]

\[1)\ Рассмотрим\ \]

\[четырехугольник\ MNKL:\]

\[MN \parallel BC \parallel LK;\]

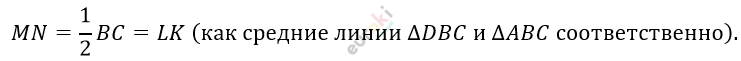
\[Следовательно:\]

\[MNKL - параллелограмм;\]

\[MK \cap LN = O;\]

\[2)\ Рассмотрим\ \]

\[четырехугольник\ MPKQ:\]

\[MP \parallel AB \parallel KQ;\ \]

\[Следовательно:\]

\[MPKQ - параллелограмм;\]

\[MK \cap PQ = O_{1};\]

\[3)\ MO_{1} = O_{1}K;\ MO = OK:\ \ \]

\[точки\ \text{O\ }и\ O_{1}\ совпадают.\]

\[4)\ Отрезки,\ соединяющие\ \]

\[середины\ сторон\ делятся\ \]

\[точкой\ пересечения\ пополам.\]

\[Что\ и\ требовалось\ доказать.\]