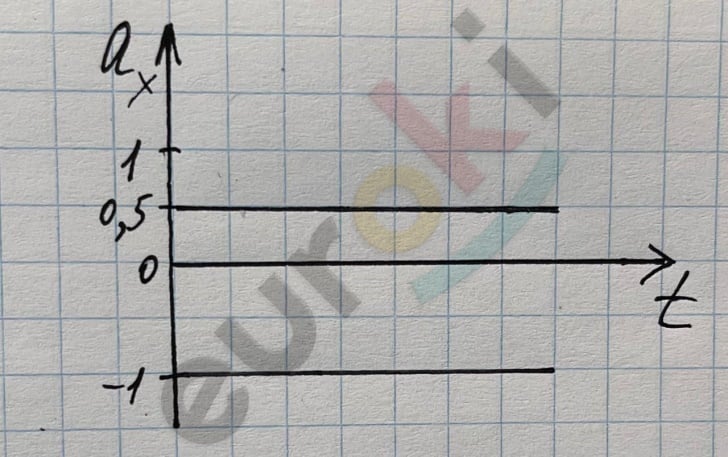ГДЗ > ⏱ Физика > 9 класс > 📗 Физика 9 класс Перышкин ФГОС, Гутник > 🧠 Задание §6

Решебник по физике 9 класс Перышкин ФГОС §6

Авторы:
Год:2023
Тип:учебник и лабораторные работы
Нужно другое издание?

§6

Скорость прямолинейного равноускоренного движения. График скорости

Стр. 30

Вопросы после параграфа

  1. Формула, по которой можно рассчитать проекцию вектора мгновенной скорости прямолинейного равноускоренного движения, если известны:

      Добавить текст Озвучить Вернуть оригинал

    а) проекция начальной скорости и проекция вектора ускорения

      Добавить текст Озвучить Вернуть оригинал

    νx = ν0x + axt ;

    б) проекция вектора ускорения при том, что начальная скорость равна нулю

      Добавить текст Озвучить Вернуть оригинал

    νx = axt .

  2. График проекции вектора скорости равноускоренного движения при начальной скорости:

      Добавить текст Озвучить Вернуть оригинал

    а) равной нулю представляет собой прямую, проходящую через начало координат;

      Добавить текст Озвучить Вернуть оригинал

    б) не равной нулю представляет собой прямую, отсекающую на оси νx отрезок, равный проекции вектора начальной скрости.

      Добавить текст Озвучить Вернуть оригинал

Обсуди с товарищем

  1. Графики, представленные на рисунках 16 и 17, это зависимости проекции вектора скорости от времени, если начальная скорость не равна нулю, однако в первом случае на рис.16 модуль вектора скорости увеличивается, а на рис.17 – уменьшается.

      Добавить текст Озвучить Вернуть оригинал

  2. На рисунке 18 тела движутся равноускоренно.

      Добавить текст Озвучить Вернуть оригинал

    Точка пересечения графиков означает одинаковую скорость движения.

      Добавить текст Озвучить Вернуть оригинал

    Модуль ускорения первого тела больше, чем у второго, так как за меньший промежуток времени модуль скорости изменяется быстрее.

      Добавить текст Озвучить Вернуть оригинал

    Закон изменения модуля скорости для тела 1: νx = 1 + t (а = \(\frac{3 - 1}{2}\) = 1 м/с2)

      Добавить текст Озвучить Вернуть оригинал

    Закон изменения модуля скорости для тела 2: νx = 4 + 0,5t (а = \(\frac{5 - 4}{2}\) = 0,5 м/с2)

      Добавить текст Озвучить Вернуть оригинал

  3. График зависимости скорости автобуса от времени:

      Добавить текст Озвучить Вернуть оригинал

Упражнение 6

Дано:

ν0 = 2 м/c

t = 4 с

a = – 0,25 м/с2

Решение:

а = \(\frac{\nu - \nu_{0}}{t}\)

ν = ν0 + axt

ν = 2 – 0,25 × 4 = 1 (м/с)

Ответ: ν = 1 м/с.
ν – ?

Дано:

ν0 = 0 м/c

ν = 2 м/c

a = 0,2 м/с2

Решение:

а = \(\frac{\nu - \nu_{0}}{t}\) = \(\frac{\nu}{t}\)

  Добавить текст Озвучить Вернуть оригинал

t = \(\frac{\nu}{a}\)

t = \(\frac{2}{0,2}\) = 10 (с)

Ответ: t = 10 с
t – ?

  1. ν = ν0 + axt

а) ν = 1 + 0,5t

t

0

1

2

3

ν

1

1,5

2

2,5

б) ν = 1 + t

t

0

1

2

3

ν

1

2

3

4

в) ν = 2 + t

t

0

1

2

3

ν

2

3

4

5

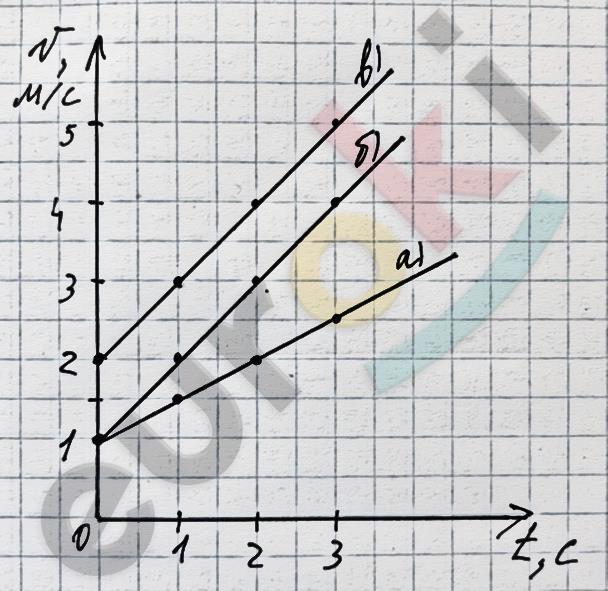
  1. ν = ν0 + axt

а) ν = 4,5 – 1,5t

t

0

1

2

3

ν

4,5

3

1,5

0

б) ν = 3 – t

t

0

1

2

3

ν

3

2

1

0

  1. На рисунке 19 тело 1 движется с ускорением по модулю:

      Добавить текст Озвучить Вернуть оригинал

    а = \(\frac{\nu - \nu_{0}}{t}\) = \(\frac{1 - 3}{4}\) = – 0,5 м/с2 .

      Добавить текст Озвучить Вернуть оригинал

    Тело 2 движется с ускорением по модулю:

    а = \(\frac{\nu - \nu_{0}}{t}\) = \(\frac{3 - 1}{2}\) = 1 м/с2 .

      Добавить текст Озвучить Вернуть оригинал

    Закон изменения модуля скорости для тела 1: νx = 3 – 0,5t

      Добавить текст Озвучить Вернуть оригинал

t

0

1

2

3

ν

3

2,5

2

1,5

Закон изменения модуля скорости для тела 2: νx = 1 + t

  Добавить текст Озвучить Вернуть оригинал

t

0

1

2

3

ν

1

2

3

4

Скачать ответ
Есть ошибка? Сообщи нам!

6
Решебники по другим предметам