ГДЗ > ⏱ Физика > 9 класс > 📗 Физика 9 класс Перышкин ФГОС, Гутник > 🧠 Задание §4

Решебник по физике 9 класс Перышкин ФГОС §4

Физика 9 класс Перышкин ФГОС, Гутник Просвещение

Содержание

Авторы:Перышкин ФГОС, Гутник

Год:2023

Тип:учебник и лабораторные работы

Нужно другое издание?

§4

Перемещение при прямолинейном равномерном движении

Стр. 19

Вопросы после параграфа

Скорость равномерного прямолинейного движения – это постоянная векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка.
Добавить текст Вернуть оригинал
Чтобы найти проекцию вектора перемещения тела, движущегося прямолинейно и равномерно, если известны проекция вектора скорости и время движения, нужно применить формулу S_x = ν_xt.
Добавить текст Вернуть оригинал
При прямолинейном движении в одном направлении модуль вектора перемещения, совершенного телом за некоторый промежуток времени равен пути, пройденному этим телом за этот же промежуток времени.
Добавить текст Вернуть оригинал
Вектор перемещения может быть меньше пути, пройденного за тот же промежуток времени, например, при движении по кругу вектор перемещения равен нулю, так как тело возвращается в первоначальную точку, а пройденный путь равен длине окружности.
Добавить текст Вернуть оригинал
По графику, изображенном на рисунке 9, можно сказать, что первое тело двигалось со скоростью 30 км/ч, а второе тело – со скоростью 25 км/ч. Так как проекция векторов скорости и перемещения первого тела положительны, а второго – отрицательны, то тела движутся в противоположных направлениях.
Добавить текст Вернуть оригинал
Для того, чтобы движение тела являлось прямолинейным равномерным, нужно, чтобы не только за любые равные промежутки времени тело проходило одинаковые пути, но и двигалось строго по прямой.
Добавить текст Вернуть оригинал

Обсуди с товарищем

Проекция на ось Х перемещения тела, движущегося параллельно этой оси, может быть по модулю равна модулю перемещения или модулю перемещения с обратным знаком – это зависит от того, в каком направлении движется тело, то есть сонаправлено его движение с осью Х или нет.
Добавить текст Вернуть оригинал
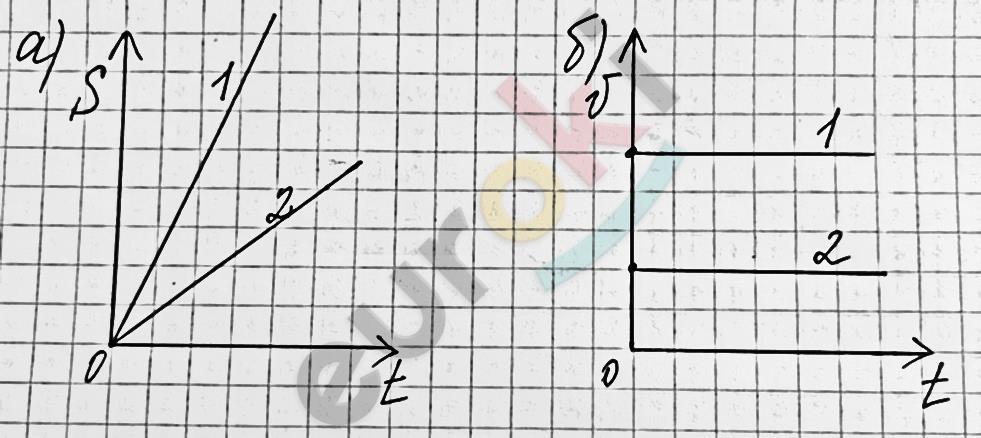
Два мотоциклиста движутся прямолинейно и равномерно, так как скорость движения первого мотоциклиста больше скорости движения второго, то на графике
  Добавить текст Вернуть оригинал
а) путей от времени линейная зависимость первого мотоциклиста будет находиться выше линейной зависимости второго мотоциклиста, то есть будет меньше угол между графиком зависимости первого тела и осью пути;
  Добавить текст Вернуть оригинал
б) скоростей от времени график зависимости первого мотоциклиста будет находиться выше графика зависимости второго мотоциклиста.
  Добавить текст Вернуть оригинал

Упражнение 4

Дано:

x₀ = 0 м

x(4c) = 20 м

Решение:

x(4с) = x₀ + ν_xt

ν_x = \(\frac{\left( x - x_{0} \right)}{t}\)

Добавить текст Вернуть оригинал

ν_x = \(\frac{(20 - 0)}{4}\) = 5 (м/с)

S = ν_xt = 5 × 5 = 25 (м)

Закон движения тела: x = 5t

Ответ: ν_x = 5 м/с, S = 25 м.

ν_x, S – ?

На рисунке 11:

- начальные координаты x₀₁ = 300 м, x₀₂ = 200 м
  Добавить текст Вернуть оригинал
- тело 1 направлено против направления движения оси x, а тело 2 сонаправлено с осью х
  Добавить текст Вернуть оригинал
- проекция скорости первого тела ν_x = \(\frac{\left( x - x_{01} \right)}{t}\) = \(\frac{(200 - 300)}{20}\) = – 5 м/с
  Добавить текст Вернуть оригинал
проекция скорости второго тела ν_x = \(\frac{\left( x - x_{02} \right)}{t}\) = \(\frac{(200 - 150)}{20}\) = 2,5 м/с
  Добавить текст Вернуть оригинал
- точка пересечения графиков означает место встречи двух тел
  Добавить текст Вернуть оригинал
- закон движения x = x₀ + ν_xt для тела 1: x = 300 – 5t
  Добавить текст Вернуть оригинал
закон движения x = x₀ + ν_xt для тела 2: x = 150 + 2,5t
  Добавить текст Вернуть оригинал
График зависимости модуля вектора скорости от времени не может располагаться под осью Ot, так как модуль вектора скорости не может быть отрицательным (т.е. скорость сама по себе, ее значение, не может быть отрицательной), а вот график проекции вектора скорости может находиться под осью Ot, поскольку знак зависит от того, сонаправлен ли график проекции вектора скорости с осью координат или нет.
Добавить текст Вернуть оригинал
Графики зависимости проекций векторов скорости от времени для трех автомобилей, движущихся прямолинейно и равномерно:
Добавить текст Вернуть оригинал
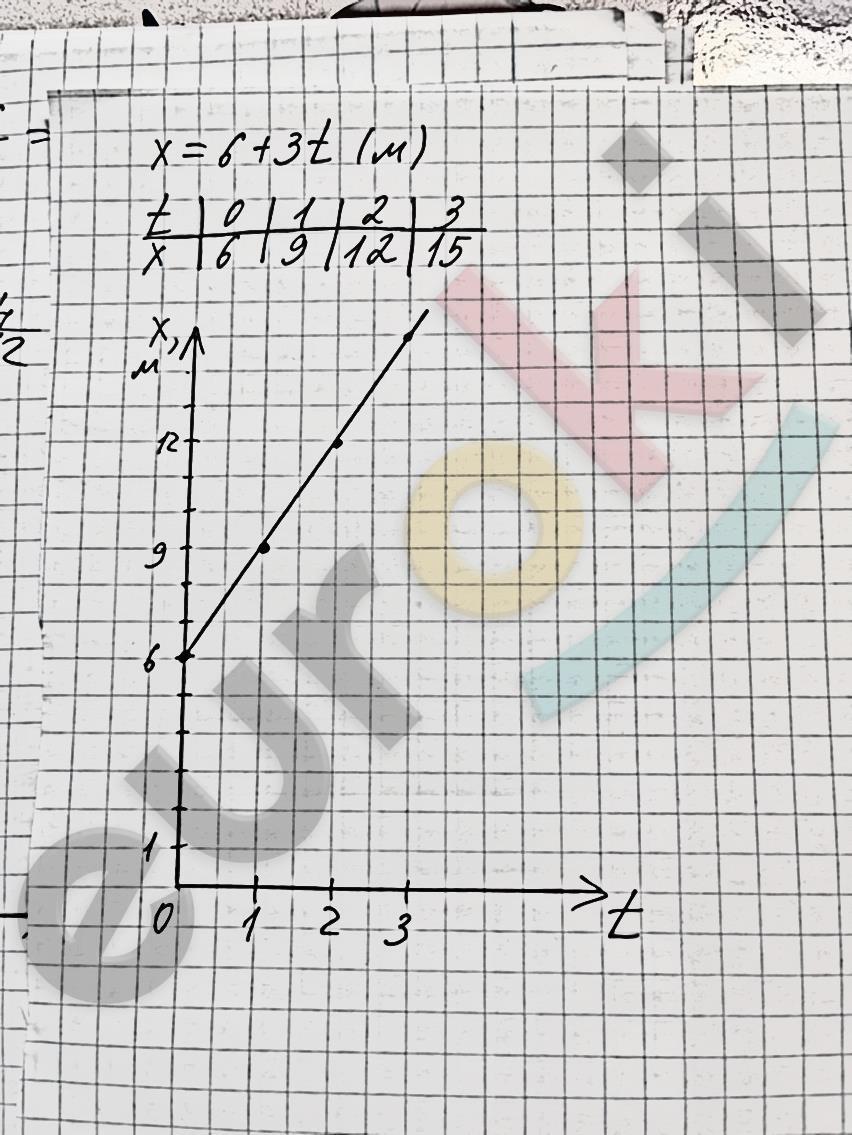
Построим график зависимости координаты от времени. Координата тела изменяется по закону x = 6 + 3t. Возьмем произвольные значения времени и подставим в уравнение, чтобы вычислить координату в этот момент времени:
Добавить текст Вернуть оригинал

t	0	1	2	3
x	6	9	12	15

Построим график:

Путь определяется по формуле S = ν_xt, а скорость равна ν_x = \(\frac{\left( x - x_{0} \right)}{t}\).

Добавить текст Вернуть оригинал

Возьмем координату x = 9 в момент времени t = 1:

Добавить текст Вернуть оригинал

ν_x = \(\frac{(9 - 6)}{1}\) = 3

Значит, путь изменяется по закону S = 3t.
Добавить текст Вернуть оригинал
Возьмем произвольные значения времени и подставим в уравнение, чтобы вычислить пройденный путь:
Добавить текст Вернуть оригинал

t	0	1	2	3
S	0	3	6	9

Построим график:

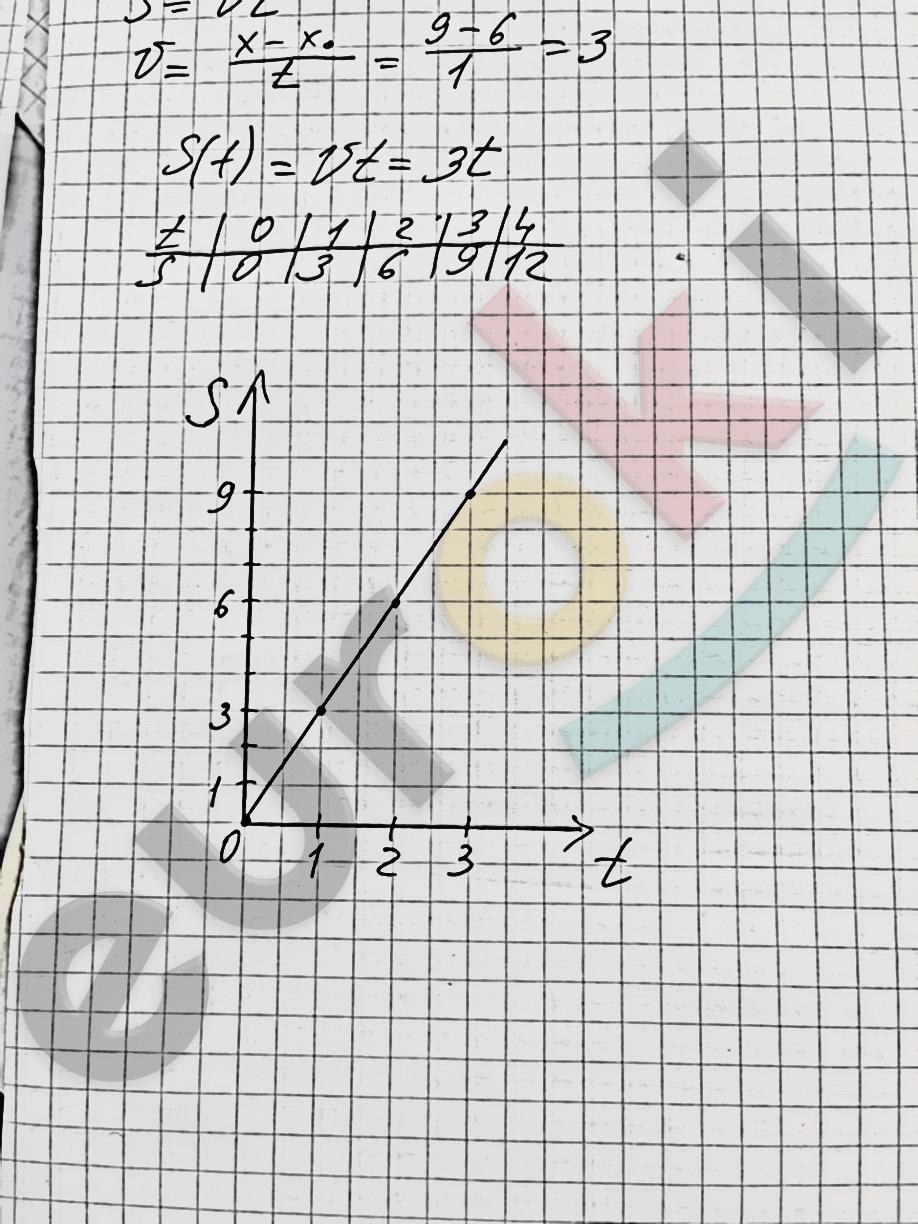
При сравнении графиков зависимости от времени координаты и пути видно, что это линейные зависимости с одинаковым углом наклона прямой. Отличие заключается в начальной координате x₀ = 6 у первого графика, что приводит к смещению прямой по оси ординат.

Добавить текст Вернуть оригинал

Задание 2