Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по физике 9 класс Перышкин ФГОС §17
§17
Сила упругости
Стр. 81
Вопросы после параграфа
-
Деформация тела возникает в том случае, когда отдельные части одного и того же тела совершают разные перемещения.
Добавить текст Вернуть оригинал -
Причиной возникновения силы упругости является сила, вызывающая деформацию тела.
Добавить текст Вернуть оригинал -
Закон Гука: возникающая при деформации сила упругости прямо пропорциональна удлинению тела: Fупр = k|x|.
Добавить текст Вернуть оригинал -
Закон Гука выполняется для случая малых упругих деформаций.
Добавить текст Вернуть оригинал -
Деформация ветки яблони вызывает появление силы упругости.
Добавить текст Вернуть оригиналДеформация поверхности наклонной плоскости вызывает появление силы упругости.
Добавить текст Вернуть оригиналДеформация пружины динамометра вызывает появление силы упругости.
Добавить текст Вернуть оригинал
Обсуди с товарищем
Упругая деформация переходит в пластическую при изменении величины силы воздействия. Так, натягивая пружину, в какой-то момент приложенная сила деформирует ее, и деформация не исчезает и после прекращения внешнего воздействия.
Добавить текст Вернуть оригиналУпражнение 17
-
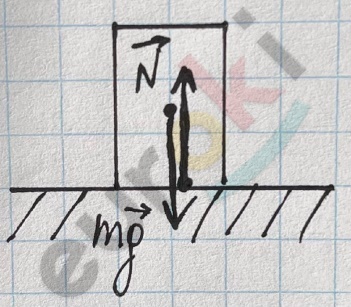
Силы, действующие на вазу, стоящую на столе: сила тяжести mg и сила реакции опоры N.
Добавить текст Вернуть оригинал
Силы, действующие на металлический шарик, подвешенный на нити: сила тяжести mg и сила натяжения нити T.
Добавить текст Вернуть оригинал
-
График зависимости деформации пружины от модуля приложенной к ней силы с учетом абсолютной погрешности:
Добавить текст Вернуть оригинал
-
|
Дано: Δx = 6 см k = 80 Н/м g = 10 м/с2 |
СИ 0,06 м |
Решение: Fупр = Fт Fупр = kΔx ; Fт = mg kΔx = mg m = \(\frac{\text{kΔx}}{g}\) m = \(\frac{80 \times 0,06}{10}\) = 0,48 (кг) = 480 (г) Добавить текст Вернуть оригиналОтвет: m = 480 г. |
|---|---|---|
| m – ? |
|
Дано: Δx = 8 см k = 50000 Н/м m = 20 т |
СИ 0,08 м 20000 кг |
Решение: Fупр = ma Fупр = kΔx kΔx = ma a = \(\frac{\text{kΔx}}{m}\) a = \(\frac{50000 \times 0,08}{20000}\) = 0,2 (м/с2) Добавить текст Вернуть оригиналОтвет: а = 0,2 м/с2. |
|---|---|---|
| a – ? |
|
Дано: m1 = 3m m2 = 2m g = 10 м/с2 |
Решение: Слева возьмем грузы за систему грузов массой 3m, а справа – за систему грузов массой 2m. Добавить текст Вернуть оригиналЗапишем второй закон Ньютона в векторной форме: Добавить текст Вернуть оригиналm1a1 = m1g + T1 m2a2 = m2g + T2 Поскольку массой нити и трением о блок можно пренебречь, силы натяжения, приложенные к грузам, можно считать равными друг другу: T1 = T2 = T Добавить текст Вернуть оригиналЕсли считать, что нить нерастяжимое, то ускорение грузов будет одинаковое: а1 = а2 = а Добавить текст Вернуть оригиналЗа положительно направление оси Y примем направление движения груза большей массы. Запишем второй закон Ньютона через проекции на ось Y: Добавить текст Вернуть оригиналm1a = m1g – T – m2a = m2g – T m1a + m2a = m1g – T – m2g + T (m1 + m2)a = (m1 – m2)g a = \(\frac{\left( m_{1} - m_{2} \right)g}{m_{1} + m_{2}}\) Добавить текст Вернуть оригиналa = \(\frac{(3m - 2m) \times 10}{3m + 2m}\) = 2 (м/с2) Добавить текст Вернуть оригиналОтвет: а = 2 м/с2. |
|---|---|
| a – ? |
