ГДЗ > ⏱ Физика > 9 класс > 📗 Физика 9 класс Перышкин ФГОС, Гутник > 🧠 Задание §14

Решебник по физике 9 класс Перышкин ФГОС §14

Авторы:
Год:2023
Тип:учебник и лабораторные работы
Нужно другое издание?

§14

Свободное падение тел

Стр. 69

Вопросы после параграфа

  1. Свободным падением называют движение тел под действием только силы тяжести.

      Добавить текст Вернуть оригинал

  2. На рисунке 41 показаны положения свободно падающего шарика, который фотографировали через каждые 0,1 с с момента начала движения. Модули векторов перемещения, совершаемых телом за последовательные равные промежутки времени при равноускоренном движении без начальной скорости, относятся как ряд последовательных нечетных чисел. Именно такой ряд и образуют соответствующие перемещения шарика, показанные на рисунке 41.

      Добавить текст Вернуть оригинал

  3. Опыт, изображенный на рисунке 42, ставился, чтобы ответить на вопрос: зависит ли ускорение при свободном падении тел от их массы, объема, формы и т.д. Из этого опыта следует вывод, что в любой момент времени все тела имеют одинаковые мгновенные скорости, а значит, движутся с одинаковым ускорением.

      Добавить текст Вернуть оригинал

  4. Ускорение свободного падения – это ускорение, придаваемое телу силой тяжести (или, иными словами, ускорение тела при свободном падении).

      Добавить текст Вернуть оригинал

  5. Сила тяжести действует на подброшенное вверх тело во время его подъема.

      Добавить текст Вернуть оригинал

  6. Тело, подброшенное вверх, при отсутствии сопротивления воздуха тоже движется с постоянным ускорением, вызванным действием силы тяжести. В этом случае начальная скорость, которую телу придали при броске, направлена вверх, т.е. противоположно силе тяжести и ускорению свободного падения. Поэтому скорость тела уменьшается (за каждую секунду – на величину, численно равную модулю ускорения свободного падения, т.е. на 9,8 м/с).

      Добавить текст Вернуть оригинал

  7. Чем бо̀льшую начальную скорость получило тело при броске, тем больше будет время подъема и тем на бо̀льшую высоту оно поднимется к моменту остановки.

      Добавить текст Вернуть оригинал

  8. При движении вверх вектор скорости тела и вектор ускорения свободного падения направлены в противоположные стороны, поэтому их проекции всегда имеют разные знаки.

      Добавить текст Вернуть оригинал

Если, к примеру, ось Х направлена вертикально вверх, т.е. сонаправлена с вектором скорости, то νх > 0, значит, νх = ν, а gx < 0, значит, gx = – g = – 9,8 м/с2.

  Добавить текст Вернуть оригинал

Если же ось X направлена вертикально вниз, то νх < 0, значит, νх = ν, а gx > 0, т.е. gx = g = 9,8 м/с2.

  Добавить текст Вернуть оригинал

  1. При определенных размерах и массе шарика сила сопротивления окажется значительно меньше силы тяжести. В этом случае равнодействующая этих двух сил мало отличается от силы Fтяж.ш. Значит, можно считать, что шарик движется с ускорением свободного падения g. Но если в воздухе падает кусочек ваты, то в этом случае сила сопротивления по модулю сравнима с силой тяжести, и равнодействующая сила Fв значительно меньше силы тяжести Fтяж.в. Поэтому кусочек ваты падает в воздухе с ускорением, гораздо меньшим ускорения свободного падения.

      Добавить текст Вернуть оригинал

  2. Галилей первым пришел к выводу о том что свободное падение является равноускоренным движением.

      Добавить текст Вернуть оригинал

Обсуди с товарищем

  1. H = \(\frac{\text{gt}^{2}}{2}\) ; t = \(\sqrt{\frac{2H}{g}}\)

      Добавить текст Вернуть оригинал

ν = gt = g\(\sqrt{\frac{2H}{g}}\) = \(\sqrt{2gH}\)

  Добавить текст Вернуть оригинал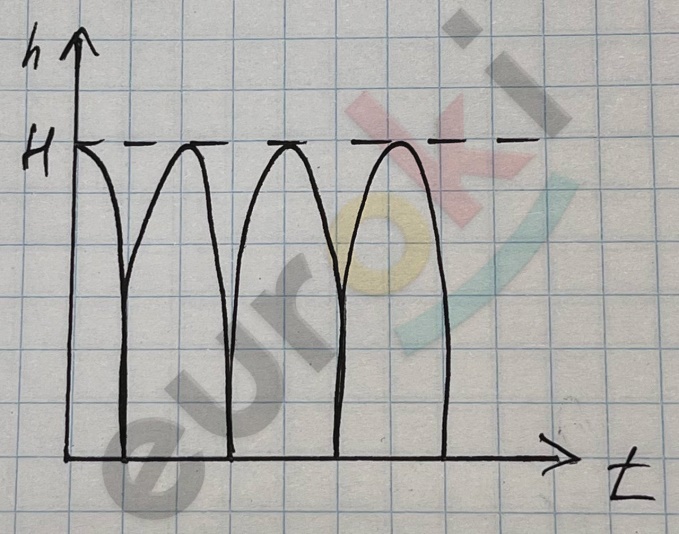

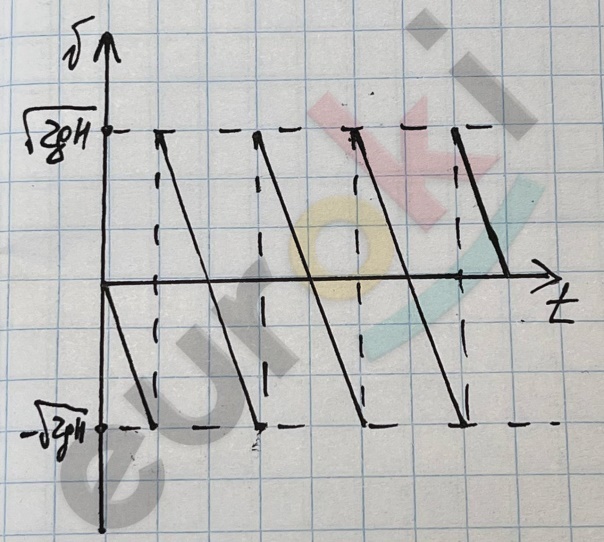
  1. А) На мяч действовала сила притяжения к Земле во время его движения как вверх, так и вниз.

      Добавить текст Вернуть оригинал

Б) Скорость мяча уменьшалась при его движении вверх, так как она направлена вверх, т.е. противоположно силе тяжести и ускорению свободного падения.

  Добавить текст Вернуть оригинал

Скорость мяча увеличивалась при его движении вниз, так как она направлена вниз, а значит, сонаправлена силе тяжести и ускорению свободного падения.

  Добавить текст Вернуть оригинал

В) При движении мяча вверх скорость уменьшалась, так как она направлена вверх, т.е. противоположно силе тяжести и ускорению свободного падения.

  Добавить текст Вернуть оригинал

При движении мяча вниз скорость увеличивалась, так как она направлена вниз, а значит, сонаправлена силе тяжести и ускорению свободного падения.

  Добавить текст Вернуть оригинал

Упражнение 14

Дано:

g = 10 м/с2

t = 2 c

Решение:

h = \(\frac{\text{gt}^{2}}{2}\)

h = \(\frac{{10 \times 2}^{2}}{2}\) = 20 (м)

  Добавить текст Вернуть оригинал

Ответ: h = 20 м.
h – ?

Дано:

h = 80 см

g = 10 м/с2

СИ

0,8 м

Решение:

h = \(\frac{\text{gt}^{2}}{2}\) ; t = \(\sqrt{\frac{2h}{g}}\)

  Добавить текст Вернуть оригинал

t = \(\sqrt{\frac{2 \times 0,8}{10}}\) = 0,4 (с)

  Добавить текст Вернуть оригинал

Ответ: t = 0,4 с.
t – ?

Дано:

h = 45 м

g = 10 м/с2

t1 = 1 c

Δt = 1 c

Решение:

h = \(\frac{\text{gt}^{2}}{2}\) ; t = \(\sqrt{\frac{2h}{g}}\)

  Добавить текст Вернуть оригинал

t = \(\sqrt{\frac{2 \times 45}{10}}\) = 3 (с)

  Добавить текст Вернуть оригинал

S1 = \(\frac{gt_{1}^{2}}{2}\) ;

Перемещение тела за последнюю секунду равно разности перемещений за все время движения и за первые две секунды:

  Добавить текст Вернуть оригинал

S2 = \(\frac{\text{gt}^{2}}{2}\) – \(\frac{{g(t - \Delta t)}^{2}}{2}\)

  Добавить текст Вернуть оригинал

S1 = \(\frac{10\ \times \ 1^{2}}{2}\) = 5 (м)

  Добавить текст Вернуть оригинал

S2 = \(\frac{10\ \times \ 3^{2}}{2}\) – \(\frac{10\ \times \ {(3 - 1)}^{2}}{2}\) = 25 (м)

  Добавить текст Вернуть оригинал

Ответ: t = 3 с, S1 = 5 м, S2 = 25 м.
t, S1, S2 – ?

Дано:

t = 2,5 с

g = 10 м/с2

Решение:

ν = gt

ν = 10 × 2,5 = 25 (м/с)

Ответ: ν = 25 м/с.
ν – ?

Дано:

h = 10 м

ν = 5 м/с

g = 10 м/с2

Решение:

ν = gt; t = \(\frac{\nu}{g}\)

t = \(\frac{5}{10}\) = 0,5 (c)

S1 = \(\frac{\text{gt}^{2}}{2}\)

S1 = \(\frac{10\ \times \ {0,5}^{2}}{2}\) = 1,25 (м) – это путь до наивысшей точки с высоты 10 м. Значит, общий пройденный путь:

  Добавить текст Вернуть оригинал

S = h + 2S1

S = 10 + 2 × 1,25 = 12,5 (м)

Ответ: S = 12,5 м.
S – ?

Дано:

ν0 = 9,8 м/с

ν = 0 м/с

g = 9,8 м/с2

Решение:

ν = ν0 – gt ; t = \(\frac{\nu_{0} - \nu}{g}\)

  Добавить текст Вернуть оригинал

t = \(\frac{9,8 - 0}{9,8}\) = 1 (с)

S = ν0t – \(\frac{\text{gt}^{2}}{2}\)

S = 9,8 × 1 – \(\frac{{9,8\ \times 1}^{2}}{2}\) = 4,9 (м)

  Добавить текст Вернуть оригинал

Ответ: t = 1 с; S = 4,9 м.
t, S – ?

  1. Тело брошено с поверхности земли вертикально вверх, останавливается в верхней точке и падает назад, поэтому ν = 0 и ν0 = gt1. Время подъема тела на максимальную высоту: t1 = \(\frac{\nu_{0}}{g}\).

      Добавить текст Вернуть оригинал

После, оно летит вниз с начальной скоростью ν’0 = 0 и скоростью падения ν2 = gt2, то есть время падения: t2 = \(\frac{\nu_{2}}{g}\) (1).

  Добавить текст Вернуть оригинал

Высота подъема в данном случае:

h = \(\frac{\nu_{0}^{2}}{2g}\) (2)

Найдем скорость падения из формулы (2):

ν2 = \(\sqrt{2gh}\) = \(\sqrt{2g\frac{\nu_{0}^{2}}{2g}}\) = ν0 (3)

  Добавить текст Вернуть оригинал

Найдем время падения, подставив в формулу (1) формулу (3):

  Добавить текст Вернуть оригинал

t2 = \(\frac{\nu_{0}}{g}\)

Значит, t1 = t2, и полное время движения: t = t1 + t2 = \(2\frac{\nu_{0}}{g}\) = 2t1

  Добавить текст Вернуть оригинал

Время полета тела до момента падения на землю вдвое больше времени его подъема на максимальную высоту: t = 2t1, что и требовалось доказать.

  Добавить текст Вернуть оригинал

Дано:

ν0 = 15 м/с

g = 10 м/с2

Решение:

В верхней точке скорость тела равна нулю, значит, высота подъема равна:

  Добавить текст Вернуть оригинал

h = \(\frac{\nu_{0}^{2}}{2g}\)

h = \(\frac{15^{2}}{2 \times 10}\) = 11,25 (м)

  Добавить текст Вернуть оригинал

Скорость в момент падения:

ν = \(\sqrt{2gh}\)

ν = \(\sqrt{2 \times 10 \times 11,25}\) = 15 (м/с)

  Добавить текст Вернуть оригинал

Ответ: ν = 15 м/с.
ν – ?
Скачать ответ
Есть ошибка? Сообщи нам!

14
Решебники по другим предметам