Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по физике 7 класс. Перышкин ФГОС Лабораторные работы
Лабораторные работы
- Лабораторная работа №1. Определение показаний измерительного прибора
- Лабораторная работа №2. Определение размеров малых тел
- Лабораторная работа №3. Измерение массы тела
- Лабораторная работа №4. Измерение объема твердого тела
- Лабораторная работа №5. Определение плотности твердого тела
- Лабораторная работа №6. Исследование силы упругости
- Лабораторная работа №7. Градуирование пружины и измерение сил динамометром
- Лабораторная работа №8. Исследование зависимости силы трения скольжения от площади соприкосновения тел, прижимающей силы, рода поверхности
- Лабораторная работа №9. Изучение выталкивающей силы, действующей на погруженное в жидкость тело
- Лабораторная работа №10. Выяснение плавания тела в жидкости
- Лабораторная работа №11. Выяснение условия равновесия рычага
- Лабораторная работа №12. Определение КПД наклонной плоскости
Лабораторная работа №1. Определение показаний измерительного прибора
Стр. 207
Цель работы: Определить цену деления шкалы измерительного цилиндра, определить с его помощью объем жидкости.
Приборы и материалы: Измерительный цилиндр, стакан с водой, небольшие сосуды.
Ход работы:
1.Общее правило для определения цены деления шкалы измерительного прибора: необходимо выбрать два соседних обозначенных штриха, вычесть из большего меньшее и разделить полученную разницу на количество делений между выбранными нами обозначенными штрихами.
Добавить текст Вернуть оригиналПредположим, что выданный учителем измерительный цилиндр рассчитан на 100 мл: верхнее значение 100 мл, нижнее – 10 мл. Тогда выбираем два соседних обозначенных штриха (у которых стоят числа) – например, 90 и 100. Между ними 10 делений. Значит цена деления С = \(\frac{100 - 90}{10}\) = 1 (мл).
Добавить текст Вернуть оригинал
| Цена деления шкалы, мл | 1 |
|---|---|
| Верхний предел измерения шкалы, мл | 100 |
| Нижний предел измерения шкалы, мл | 10 |
2.Приступаем к определению объема налитой жидкости.
Важно! Для уменьшения погрешности измерения следует глаз располагать на уровне, совпадающем с плоской частью поверхности жидкости.
Добавить текст Вернуть оригиналНаливаем некоторое количество воды из наполненного до краев стакана в измерительный цилиндр. Например, получили 53 мл.
Добавить текст Вернуть оригинал3.Определим вместимость стакана. Доливаем в измерительный цилиндр оставшуюся в стакане воду. Например, получили 70 мл.
4.Записываем данные в таблицу. Строка первая.
Измерения записываются с учетом абсолютной погрешности, она равна половине цены деления ΔV = \(\frac{С}{2}\) . ΔV = \(\frac{1}{2}\) = 0,5 (мл).
Добавить текст Вернуть оригинал5.Так же с помощью выданного учителем измерительного цилиндра определяем вместимость других сосудов, которые вам выдал учитель.
Добавить текст Вернуть оригиналВсе приведенные значения взяты в качестве образца. По образу и подобию повторите опыт со своими значениями.
Добавить текст Вернуть оригинал| № опыта | Название сосуда |
Объем жидкости Vж ± ΔV, мл |
Вместимость сосуда Vс ± ΔV, мл |
|---|---|---|---|
| 1 | Стакан | 53,0 ± 0,5 | 70,0 ± 0,5 |
| 2 | Сосуд 1 | 24,0 ± 0,5 | 50,0 ± 0,5 |
| 3 | Сосуд 2 | 69,0 ± 0,5 | 90,0 ± 0,5 |
Вывод: Цена деления измерительного цилиндра составляет 1 мл; с учетом абсолютной погрешности, равной 0,5 мл, объем жидкости равен 53,0 ± 0,5 мл; вместимость сосудов – 70,0 ± 0,5 мл.
Добавить текст Вернуть оригиналЛабораторная работа №2. Определение размеров малых тел
Стр. 208
Цель работы: Определить размеры малых тел способом рядов.
Приборы и материалы: Линейка ученическая, горох, пшено (или круглые бусины, бисер), иголка.
Ход работы:
1. Нужно вычислить диаметр одной горошины. Положим вплотную к линейке 30 горошин в ряд. Получили длину ряда l = 176 мм. Делим ее на число N горошин в ряду d = \(\frac{l}{N}\) = \(\frac{176}{30}\) = 5,87 мм.
Добавить текст Вернуть оригинал2. Результаты измерений записываем в таблицу с учетом абсолютной погрешности. Абсолютная погрешность измерения длины ряда равна цене деления шкалы линейки. Цена деления линейки равна C = \(\frac{1 - 0}{10}\) = 0,1 см = 1 мм. Значит, абсолютная погрешность измерения длины ряда равна Δl = 1 мм.
Добавить текст Вернуть оригиналАбсолютная погрешность измерения диаметра горошины будет в N раз меньше, то есть Δd = \(\frac{\Delta l}{N}\) = \(\frac{1}{30}\) = 0,03 мм. Это первая строка таблицы.
Добавить текст Вернуть оригинал3. Определяем методом рядов размер крупинки пшена. Так же положили 30 крупинок в ряд вплотную к линейке. Получили длину ряда l = 31 мм. Делим ее на число N крупиц пшена в ряду d = \(\frac{l}{N}\) = \(\frac{31}{30}\) = 1,03 мм. Абсолютные погрешности остаются такими же. Это вторая строка таблицы.
Добавить текст Вернуть оригинал4. Увеличим количество крупинок пшена в два раза (N = 60). Получили длину ряда l = 63 мм. Делим ее на число N крупиц пшена в ряду d = \(\frac{l}{N}\) = \(\frac{63}{60}\) = 1,05 мм. Абсолютная погрешность измерения длины ряда равна остается той же Δl = 1 мм. Абсолютная погрешность измерения диаметра горошины будет в N раз меньше, то есть Δd = \(\frac{\Delta l}{N}\) = \(\frac{1}{60}\) = 0,02 мм.
Добавить текст Вернуть оригинал| № опыта | Число частиц в ряду |
Длина ряда l ± Δl, мм |
Размер одной частицы d ± Δd, мм |
|---|---|---|---|
| 1 (горох) | 30 | 176 ± 1 | 5,87 ± 0,03 |
| 2 (пшено) | 30 | 31 ± 1 | 1,03 ± 0,03 |
| 3 (пшено) | 60 | 63 ± 1 | 1,05 ± 0,02 |
Вывод: мы определили размеры малых тел способом рядов. Этот метод действительно легок и удобен в использовании, когда нужно измерить размер крайне малого тела.
Добавить текст Вернуть оригиналДополнительное задание
Способом рядов определяем диаметр молекулы золота по фотографии.
Добавить текст Вернуть оригиналВозьмем ряд длиной l = 2 см = 20 мм
Делим длину ряда на число молекул N = 12 и получаем диаметр одной частицы:
Добавить текст Вернуть оригиналd = \(\frac{l}{N}\) = \(\frac{20}{12}\) = 1,7 мм.
Добавить текст Вернуть оригиналЧтобы найти истинный размер одной частицы, нужно размер на фотографии разделить на увеличение фотографии (на 5 миллионов):
Добавить текст Вернуть оригиналdист = \(\frac{1,7}{5000000}\) = 0,00000034 мм
Добавить текст Вернуть оригинал| Число частиц в ряду | Длина ряда l, мм |
Размер одной частицы d, мм |
|
|---|---|---|---|
| На фотографии | Истинный | ||
| 12 | 20 | 1,7 | 0,00000034 |
Вывод: с помощью способа рядов мы определили диаметр молекулы золота.
Лабораторная работа №3. Измерение массы тела
Стр. 210
Цель работы: Измерить массу тела с помощью весов.
Приборы и материалы: Весы рычажные с разновесами, электронные весы, несколько небольших тел разной массы.
Ход работы:
1. Перед началом взвешивания проверьте, что весы уравновешены. На левую чашу весов кладем взвешиваемое тело, на правую ставим гири, начиная с большей. Методом подбора добились равновесия.
Добавить текст Вернуть оригинал2. Результаты записываем в таблицу. Абсолютная погрешность равна массе наименьшего разновеса на чаше весов.
| № опыта | Название тела | Масса гирь, которыми уравновешено тело |
Масса тела m ± Δm, г |
|---|---|---|---|
| 1 | Тело 1 | 5 г, 200 мг, 10 мг | 5,21 ± 0,01 |
| 2 | Тело 2 | 1г, 200 мг, 100 мг | 1,3 ± 0,1 |
| 3 | Тело 3 | 100г, 5 г, 10 мг | 105,01 ± 0,01 |
3. Проводим измерения массы этих же тел с помощью электронных весов. Измерения проводим не менее трех раз.
4. Необходимо вычислить среднее значение массы mср по результатам многократных измерений по формуле mср = \(\frac{m1 + \ m2 + \ m3}{3}\)
Добавить текст Вернуть оригиналВозьмем в пример первое тело:
mср = \(\frac{5,221 + \ 5,222 + \ 5,223}{3}\) = 5,2213 г
Добавить текст Вернуть оригиналЧтобы найти Δmср, определяем отклонение каждого результата от среднего арифметического (В ТАБЛИЦУ ЭТИ ОТКЛОНЕНИЯ НЕ ПОЙДУТ, ТОЛЬКО Δmср):
Добавить текст Вернуть оригиналΔm1 = |mср – m1| = |5,2213 – 5,221| = |0,0003| = 0,0003 (г)
Добавить текст Вернуть оригиналΔm2 = |mср – m2| = |5,2213 – 5,222| = |-0,0007| = 0,0007 (г)
Добавить текст Вернуть оригиналΔm3 = |mср – m3| = |5,2213 – 5,221| = |0,0003| = 0,0003 (г)
Добавить текст Вернуть оригиналЗатем определяем Δmср = \(\frac{\text{Δm}1 + \ \text{Δm}2 + \text{Δm}3}{3}\)
Добавить текст Вернуть оригиналΔmср = \(\frac{\text{Δm}1 + \ \text{Δm}2 + \text{Δm}3}{3}\) = \(\frac{0,0003 + \ 0,0007 + 0,0003}{3}\) = 0,0004 (г)
Добавить текст Вернуть оригиналАбсолютная погрешность Δm указана в паспорте весов (скорее всего у вас будет либо 1 мг, либо 0,01 г). Я возьму 1 мг = 0,001 г. ВЫ БЕРЕТЕ ОГРЕШНОСТЬ, НАПИСАННУЮ В ПАСПОРТЕ ПРИБОРА, КОТОРЫЙ ВАМ ВЫДАСТ УЧИТЕЛЬ.
Добавить текст Вернуть оригинал| Название тела | m1 ± Δm, г | m2 ± Δm, г | m3 ± Δm, г | mср ± Δmср, г |
|---|---|---|---|---|
| Тело 1 | 5,221 ± 0,001 | 5,222 ± 0,001 | 5,221 ± 0,001 | 5,2210 ± 0,0004 |
То же самое проделайте с телом 2 и телом 3.
Добавить текст Вернуть оригиналВывод: сравнив результаты измерений на учебных и электронных весах, получили, что в случае с электронными весами провести измерения получилось с большей точностью, погрешность оказалась на два порядка меньше, чем у рычажных весов с разновесами.
Добавить текст Вернуть оригиналЛабораторная работа №4. Измерение объема твердого тела
Стр. 211
Цель работы: Измерить объем твердого тела с помощью измерительного цилиндра.
Приборы и материалы: Измерительный цилиндр, металлический брусок, тела неправильной формы небольшого объема (гайки, пластиковые игрушки, кусочки металла и др.), нитки.
Добавить текст Вернуть оригиналХод работы:
1.Определяем цену деления шкалы измерительного цилиндра. Выбираем два соседних обозначенных штриха, вычитаем из большего меньшее и делим полученную разницу на количество делений между выбранными нами обозначенными штрихами. С = \(\frac{135 - 130}{5}\) = 1 мл = 1 см3.
Добавить текст Вернуть оригинал2. Наливаем воду в измерительный цилиндр, допустим, это будет V1 = 78 мл = 78 см3.
3. Опускаем брусок полностью в воду. Объем воды и бруска V2 = 98 мл = 98 см3. Определяем объем бруска V = V2 – V1 = 98 – 78 = 20 мл = 20 см3.
Добавить текст Вернуть оригинал4. Длина бруска равна a = 4,6 см
Ширина бруска b = 2,5 см
Высота бруска c = 1,7 см
V = abc = 4,6 × 2,5 × 1,7 = 19,55 см3
5. ΔV1 = С = 1 см3
ΔV2= С = 1 см3
ΔV = ΔV1 + ΔV2 = 1+1 = 2 см3
| № опыта | Название тела/части тела | Объем воды в измерительном цилиндре V1 ± ΔV1, см3 |
Объем воды и тела/части тела V2 ± ΔV2, см3 |
Объем тела/части тела V ± ΔV, см3 |
Рассчитанный объем тела/части тела V, см3 |
|---|---|---|---|---|---|
| 1 | брусок | 78 ± 1 | 98 ± 1 | 20 ± 2 | 19,55 |
6. Объем воды в измерительном цилиндре V1 = 78 мл = 78 см3.
Объем воды с опущенным наполовину V2 = 88 мл = 88 см3. Определяем объем половины бруска V = V2 – V1 = 88 – 78 = 10 мл = 10 см3.
Добавить текст Вернуть оригинал7. Длина бруска равна a = 2,3 см
Ширина бруска b = 2,5 см
Высота бруска c = 1,7 см
V = abc = 2,3 × 2,5 × 1,7 = 9,78 см3
Объемы с учетом погрешности получились равными.
Добавить текст Вернуть оригиналВывод: мы научились измерять объем твердого тела с помощью измерительного цилиндра: для этого необходимо определить разницу между начальным объемом воды в измерительном цилиндре и объемом воды с погруженным в нее телом.
Добавить текст Вернуть оригиналДополнительное задание:
Заполняем воду в отливной сосуд, пока она не начнет течь из носика в стоящий рядом сосуд. Ждем, пока вода не перестанет течь. Излишки вылившейся воды в стоящем рядом сосуде убираем. Затем погружаем в отливной сосуд тело неправильной формы. Вода выльется из носика в стоящий рядом пустой сосуд. Объем вытесненной воды будет равен объему погруженного тела. Далее переливаем вытесненную воду в измерительный цилиндр и по шкале смотрим, каким объемом обладает наше тело.
Добавить текст Вернуть оригиналЛабораторная работа №5. Определение плотности твердого тела
Стр. 213
Цель работы: Определить плотность вещества твердого тела с помощью весов и измерительного цилиндра.
Приборы и материалы: Весы рычажные с разновесами, измерительный цилиндр, твердое тело неизвестной плотности, нить.
Ход работы:
1. С помощью рычажных весов с разновесами определяем массу тела. Сначала нужно добиться равновесия весов. Затем на левую чашу ставим тело и уравновешиваем ее разновесами на правой чаше. Поставили разновесы массой 50 г, 10 г и 5 г.
Добавить текст Вернуть оригиналm = 50 + 10 + 5 = 65 г.
Абсолютная погрешность равна массе наименьшего разновеса на чаше весов: Δm = 5 г.
Добавить текст Вернуть оригинал2. Записываем в таблицу.
3. С помощью измерительного цилиндра измеряем объем тела. Первоначальный объем воды V1 = 78 мл = 78 см3. Объем воды с опущенным телом V2 = 103 мл = 103 см3. Определяем объем половины бруска V = V2 – V1 = 103 – 78 = 25 мл = 25 см3.
Добавить текст Вернуть оригиналАбсолютная погрешность:
ΔV1 = С = 1 см3
ΔV2= С = 1 см3
ΔV = ΔV1 + ΔV2 = 1+1 = 2 см3
| Масса тела m ± Δm, г |
Объем тела V ± ΔV, см3 |
Плотность вещества ρ | |
|---|---|---|---|
| \[\frac{г}{см3}\] | \[\frac{кг}{м3}\] | ||
| 65 ± 5 | 25 ± 2 | 2,5 | 2500 |
По формуле ρ = \(\frac{m}{V}\) считаем плотность вещества, из которого сделано тело: ρ = \(\frac{65}{25}\) = 2,5 г/см3 = 2500 кг/м3.
Добавить текст Вернуть оригиналЭто может быть тело из бетона.
Вывод: мы определили плотность вещества твердого тела, измерив массу на рычажных весах и объем – в измерительном цилиндре.
Добавить текст Вернуть оригиналЛабораторная работа №6. Исследование силы упругости
Стр. 214
Цель работы: Проверить справедливость гипотезы: «При небольших деформациях сила упругости прямо пропорциональна удлинению пружины».
Добавить текст Вернуть оригиналПриборы и материалы: Штатив с муфтой и лапкой, спиральная пружина, набор грузов массой 100 г каждый, линейка.
Ход работы:
Длина пружины в ненагруженном состоянии l0 = 5,5 см.
Добавить текст Вернуть оригиналПодвешивая к пружине последовательно грузы массой 100 г каждый, получаем, что длина нагруженной пружины, удлинение x = l – l0 и сила упругости Fупр= nFтяж = nmg (где n – число грузов) равны:
Добавить текст Вернуть оригиналс одним грузом l = 8 см; x = 8 – 5,5 = 2,5 см; Fупр= 1 × 0,1 × 10 = 1 Н
Добавить текст Вернуть оригиналс двумя грузами l = 10,5 см; x = 10,5 – 5,5 = 5 см; Fупр= 2 × 0,1 × 10 = 2 Н
Добавить текст Вернуть оригиналс тремя грузами l = 13 см; x = 13 – 5,5 = 7,5 см; Fупр= 3 × 0,1 × 10 = 3 Н
Добавить текст Вернуть оригиналс четырьмя грузами l = 15,5 см; x = 15,5 – 5,5 = 10 см; Fупр= 4 × 0,1 × 10 = 4 Н
Добавить текст Вернуть оригиналЦена деления линейки равна C = \(\frac{1 - 0}{10}\) = 0,1 см. Значит, абсолютная погрешность измерения Δl0 = Δl = 0,1 см.
Добавить текст Вернуть оригиналАбсолютная погрешность Δx = Δl0 + Δl = 0,1 + 0,1 = 0,2 см
Добавить текст Вернуть оригинал| Число грузов | Начальная длина пружины l0 ± Δl0, см |
Длина нагруженной пружины l ± Δl, см |
Сила упругости пружины Fупр |
Удлинение x ± Δx, см |
Отношение удлинений и сил упругости | |
|---|---|---|---|---|---|---|
| \[\frac{x}{x_{1}}\] | \[\frac{F_{упр}}{F_{упр1}}\] | |||||
| 1 | 5,5 ± 0,1 | 8,0 ± 0,1 | 1 | 2,5 ± 0,2 | – | – |
| 2 | 10,5 ± 0,1 | 2 | 5,0 ± 0,2 | 2 | 2 | |
| 3 | 13,0 ± 0,1 | 3 | 7,5 ± 0,2 | 3 | 3 | |
| 4 | 15,5 ± 0,1 | 4 | 10,0 ± 0,2 | 4 | 4 | |
Найдем отношение удлинения пружины для двух, трех и четырех грузов к удлинению пружины с одним грузом \(\frac{x}{x_{1}}\):
Добавить текст Вернуть оригиналдля двух грузов: \(\frac{5}{2,5}\) = 2
для трех грузов: \(\frac{7,5}{2,5}\) = 3
Добавить текст Вернуть оригиналдля четырех грузов: \(\frac{10}{2,5}\) = 4
Добавить текст Вернуть оригиналНайдем отношение сил упругости пружины с двумя, тремя, четырьмя грузами к силе упругости пружины с одним грузом \(\frac{F_{упр}}{F_{упр1}}\):
Добавить текст Вернуть оригиналс двумя грузами: \(\frac{2}{1}\) = 2
с тремя грузами: \(\frac{3}{1}\) = 3
с четырьмя грузами: \(\frac{4}{1}\) = 4
Получили, что действительно при небольших деформациях сила упругости прямо пропорциональна удлинению пружины. В таблице видна прямая зависимость.
Добавить текст Вернуть оригиналВывод: на основе полученных результатов можно сделать вывод, что гипотеза «При небольших деформациях сила упругости прямо пропорциональна удлинению пружины» справедлива.
Добавить текст Вернуть оригиналЛабораторная работа №7. Градуирование пружины и измерение сил динамометром
Стр. 215
Цель работы: Проградуировать пружину, получить шкалу с заданной ценой деления и с помощью созданного динамометра измерить силы.
Добавить текст Вернуть оригиналПриборы и материалы: Динамометр, шкала которого закрыта бумагой, набор грузов массой 100 г каждый, штатив с муфтой и лапкой, линейка, груз неизвестной массы.
Добавить текст Вернуть оригиналХод работы:
1. Укрепили динамометр с закрытой шкалой в лапке штатива вертикально. На бумаге отметили начальное положение указателя – это будет нулевая отметка шкалы.
Добавить текст Вернуть оригинал
2. Подвесим к крючку динамометра груз массой 100 г, считая, что на один груз действует сила тяжести 1 Н. Затем довешиваем второй груз, третий и четвертый.
Добавить текст Вернуть оригиналПоложения указателя отмечаем штрихом.
3. Затем оцифруем горизонтальные штрихи, начиная с верхнего, проставив числа 0, 1, 2, 3, 4. Выше полученной шкалы указываем единицы измерения.
Добавить текст Вернуть оригинал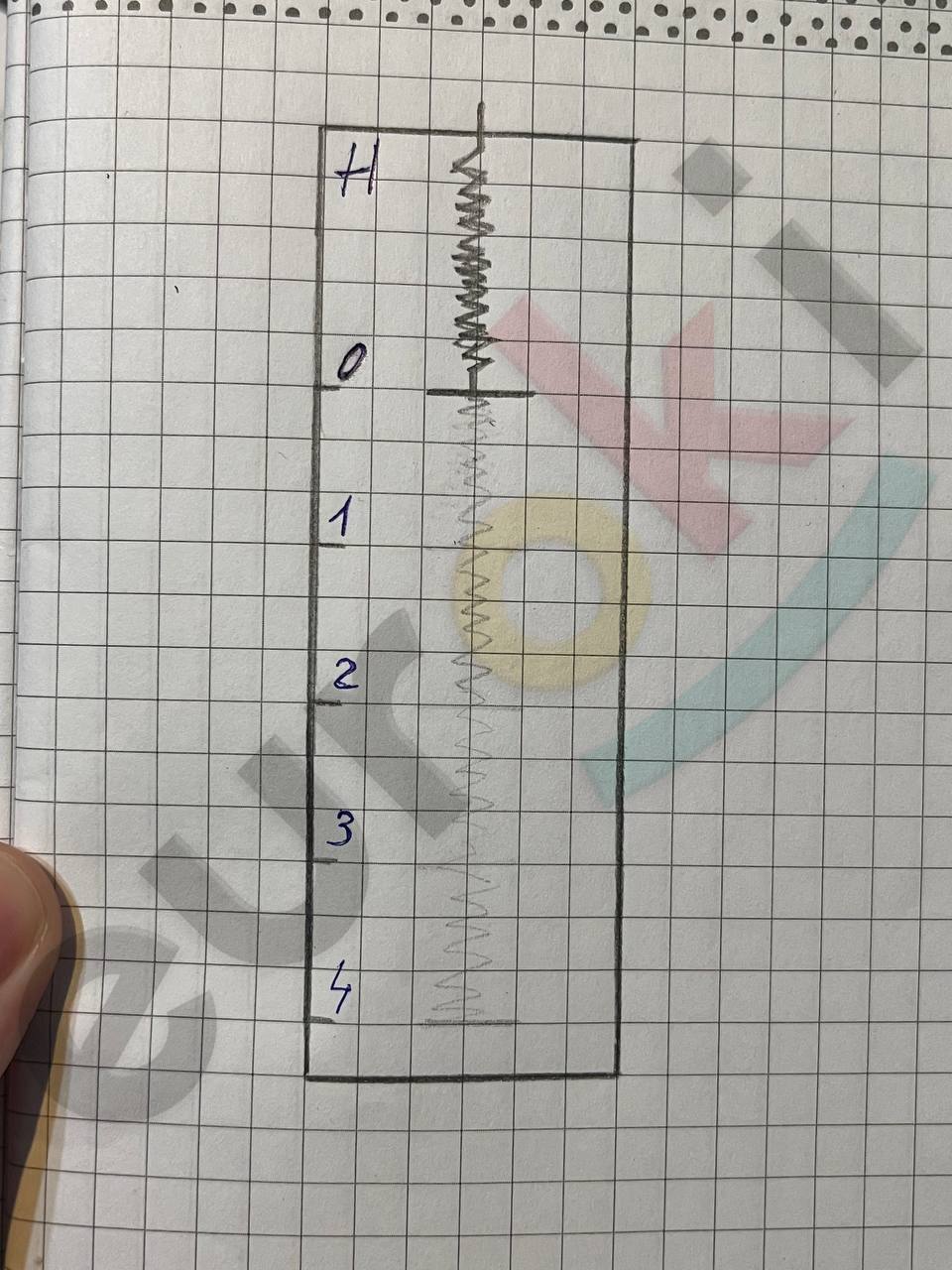
4. С помощью линейки делим расстояние между штрихами, чтобы цена деления шкалы была равна 0,1 Н. Чтобы найти количество делений, нужно выбрать два рядом стоящих штриха, из большего вычесть меньшее и разделить на цену деления 0,1 Н: n = \(\frac{4 - 1}{0,1}\) = 10 делений.
Добавить текст Вернуть оригинал
5. Проградуированным динамометром измеряем вес груза. Измерили вес груза массой 250 г, получили P = 2,5 Н.
Вывод: мы проградуировали пружину, получили шкалу с заданной ценой деления и с помощью созданного динамометра измерили силы.
Добавить текст Вернуть оригиналЛабораторная работа №8. Исследование зависимости силы трения скольжения от площади соприкосновения тел, прижимающей силы, рода поверхности
Стр. 216
Цель работы: Исследовать зависимость силы трения скольжения от площади соприкосновения тел, прижимающей силы и рода поверхности.
Добавить текст Вернуть оригиналПриборы и материалы: Динамометр, деревянный брусок, набор грузов массой 100 г каждый, деревянная и пластиковая рейки.
Ход работы:
1. Определим вес бруска с помощью динамометра: P = 0,5 Н.
2. Запишем результат в таблицу. Абсолютная погрешность равна цене деления шкалы динамометра: ΔP = ΔF = С = \(\frac{2 - 1}{10}\) = 0,1(Н)
Добавить текст Вернуть оригинал| № опыта | Сила трения Fтр ± ΔF, Н |
Вес тела P ± ΔP, Н |
|
|---|---|---|---|
| Широкая грань бруска | Узкая грань бруска | ||
| 1 | 0,2 ± 0,1 | 0,2 ± 0,1 | 0,5 ± 0,1 |
| 2 | 0,5 ± 0,1 | 0,5 ± 0,1 | 1,5 ± 0,1 |
| 3 | 0,8 ± 0,1 | 0,8 ± 0,1 | 2,5 ± 0,1 |
3. Положим брусок на деревянную рейку широкой гранью и с помощью динамометра измерим силу тяги: Fтр = 0,2 Н.
4. Положим брусок на доску узкой гранью и с помощью динамометра измерим силу трения скольжения: Fтр = 0,2 Н.
5. Нагружая брусок поочередно одним, а затем двумя, повторим измерения.
С одним грузом: Измеряем вес бруска вместе с весом груза: P = 1,5 Н. Измеряем на большей грани силу трения: Fтр = 0,5 Н. Измеряем на меньшей грани силу трения: Fтр = 0,5 Н.
Добавить текст Вернуть оригиналС двумя грузами: Измеряем вес бруска вместе с весом грузов: P = 2,5 Н. Измеряем на большей грани силу трения: Fтр = 0,8 Н. Измеряем на меньшей грани силу трения: Fтр = 0,8 Н.
Добавить текст Вернуть оригинал7. Повторяем пункты, начиная с третьего, заменив деревянную рейку пластиковой. Нужно прийти к выводу, что сила трения зависит от рода поверхности.
Добавить текст Вернуть оригиналВывод: на основе полученных результатов пришли к выводу, что сила трения скольжения зависит прижимающей силы и рода поверхности, однако не зависит от площади соприкосновения тел.
Добавить текст Вернуть оригиналЛабораторная работа №9. Изучение выталкивающей силы, действующей на погруженное в жидкость тело
Стр. 217
Цель работы: Исследовать зависимость выталкивающей силы, действующей на погруженное в жидкость тело, от плотности жидкости и объема погруженной части тела.
Добавить текст Вернуть оригиналПриборы и материалы: Динамометр, штатив с муфтой и лапкой, нить, два тела разного объема, два тела одинакового объема разной массы, стаканы с водой и насыщенным раствором поваренной соли в воде.
Добавить текст Вернуть оригиналХод работы:
1. Подвесим на динамометр тело и измерим его вес в воздухе: PV1 = 0,7 Н.
2. Подставим стакан с водой и опустим муфту с лапкой и динамометром так, чтобы все тело оказалось под водой; снимем показание динамометра: вес тела в воде P1V1 = 0,5 Н.
Добавить текст Вернуть оригинал3. По полученным данным вычисляем выталкивающую силу FV1 = PV1 – P1V1:
FV1 = 0,7 – 0,4 = 0,3 Н.
4. Записываем измерения в таблицу. Абсолютная погрешность ΔP равна цене деления динамометра: ΔP = С = \(\frac{2 - 1}{10}\) = 0,1 Н
Добавить текст Вернуть оригиналАбсолютная погрешность измерения выталкивающей силы равна ΔF = 2ΔP:
Добавить текст Вернуть оригиналΔF = 2 × 0,1 = 0,2 Н
5. Опускаем тело в насыщенный раствор соли: вес тела в насыщенном растворе соли P1V1 = 0,4 Н; выталкивающая сила тела в насыщенном растворе соли FV1 = 0,7 – 0,4 = 0,3 Н
Добавить текст Вернуть оригинал| Жидкость |
Вес тела в воздухе P ± ΔP, Н |
Вес тела в жидкости P1 ± ΔP, Н |
Выталкивающая сила F ± ΔF, Н |
|||
|---|---|---|---|---|---|---|
| PV1 | PV2 | P1V1 | P1V2 | FV1 | FV2 | |
| Вода | 0,7 ± 0,1 | 0,9 ± 0,1 | 0,5 ± 0,1 | 0,6 ± 0,1 | 0,2 ± 0,2 | 0,3 ± 0,2 |
| Насыщенный раствор соли в воде | 0,7 ± 0,1 | 0,9 ± 0,1 | 0,4 ± 0,1 | 0,5 ± 0,1 | 0,3 ± 0,2 | 0,4 ± 0,2 |
6. То же самое проделываем со вторым грузом: вес тела в воздухе PV2 = 0,9 Н; вес тела в воде P1V2 = 0,6; выталкивающая сила FV2 = 0,9 – 0,6 = 0,3 Н.
Добавить текст Вернуть оригиналВес тела в насыщенной раствор соли: P1V1 = 0,5 Н; выталкивающая сила FV2 = 0,9 – 0,5 = 0,4 Н.
Добавить текст Вернуть оригиналВывод: проанализировав результаты, мы сделали выводы, что выталкивающая сила возрастает с увеличением объема погруженной части тела, а так же зависит от плотности жидкости: с увеличением плотности жидкости, увеличивается и выталкивающая сила.
Добавить текст Вернуть оригиналДополнительное задание 1: выталкивающая сила не будет зависеть от массы и плотности тела.
Дополнительное задание 2: выталкивающая сила будет зависеть от объема погруженной части тела: выталкивающая сила возрастает с увеличением объема погруженной части тела.
Добавить текст Вернуть оригиналЛабораторная работа №10. Выяснение плавания тела в жидкости
Стр. 219
Цель работы: Исследовать явление плавания тел в жидкости.
Приборы и материалы: Весы рычажные с разновесами, измерительный цилиндр, пробирка (аптечный пузырек) с пробкой, проволочный крючок, сухой песок, фильтровальная бумага или сухая тряпка.
Добавить текст Вернуть оригиналХод работы:
1. Погружаем пробирку с песком в воду, чтобы она частично погрузилась:
объем вытесненной воды V = 14 мл = 14 см3 = 0,000014 м3
Добавить текст Вернуть оригиналвыталкивающая сила FА = ρжVп.ч.g = 1000 кг/м3 × 9,8 Н/кг × 0,000014 м3 = 0,14
Добавить текст Вернуть оригиналмасса равна сумме масс разновесов 10 г, 1г, 1 г, 1г: m = 10+1+1+1 = 13 г = 0,013 кг
Добавить текст Вернуть оригиналсила тяжести пробирки с песком: Fтяж = mg = 0,013 × 9,8 = 0,13 Н
Добавить текст Вернуть оригиналАбсолютная погрешность объема равна цене деления измерительного цилиндра: ΔV = С = 2 мл = 2 см3 = 0,000002 м3.
Добавить текст Вернуть оригиналАбсолютная погрешность массы пробирки с песком равна массе наименьшего разновеса на чаше весов: Δm = 1 г = 0,001 кг.
Добавить текст Вернуть оригинал2. Добавляем песок в пробирку, чтобы пробирка полностью погрузилась в воду (плавает):
объем вытесненной воды V = 20 мл = 20 см3 = 0,00002 м3
Добавить текст Вернуть оригиналвыталкивающая сила FА = ρжVп.ч.g = 1000 кг/м3 × 9,8 Н/кг × 0,00002 м3 = 0,2 Н
Добавить текст Вернуть оригиналмасса равна сумме масс разновесов 20 г, 1г, 1 г,: m = 20+1+1= 22 г = 0,022 кг
Добавить текст Вернуть оригиналсила тяжести пробирки с песком: Fтяж = mg = 0,022× 9,8 = 0,22 Н
Добавить текст Вернуть оригиналАбсолютная погрешность объема равна цене деления измерительного цилиндра: ΔV = С = 2 мл = 2 см3 = 0,000002 м3.
Добавить текст Вернуть оригиналАбсолютная погрешность массы пробирки с песком равна массе наименьшего разновеса на чаше весов: Δm = 1 г.
Добавить текст Вернуть оригинал3. Добавляем еще песок в пробирку, чтобы она опустилась на дно:
объем вытесненной воды V = 20 мл = 20 см3 = 0,00002 м3
Добавить текст Вернуть оригиналвыталкивающая сила FА = ρжVп.ч.g = 1000 кг/м3 × 9,8 Н/кг × 0,00002 м3 = 0,2 Н
Добавить текст Вернуть оригиналмасса равна сумме масс разновесов 20 г, 5г, 1 г, 1 г, 1г: m = 20+5+1+1+1 = 28 г = 0,028 кг
Добавить текст Вернуть оригиналсила тяжести пробирки с песком: Fтяж = mg = 0,028 × 9,8 = 0,28 Н
Добавить текст Вернуть оригиналАбсолютная погрешность объема равна цене деления измерительного цилиндра: ΔV = С = 2 мл = 2 см3 = 0,000002 м3.
Добавить текст Вернуть оригиналАбсолютная погрешность массы пробирки с песком равна массе наименьшего разновеса на чаше весов: Δm = 1 г.
Добавить текст Вернуть оригинал| № опыта |
Масса пробирки с песком m ± Δm, кг |
Сила тяжести пробирки с песком Fтяж, Н |
Объем вытесненной воды V ± ΔV, м3 |
Выталкивающая сила, действующая на пробирку Добавить текст Вернуть оригиналFА, Н |
Поведение пробирки в воде |
|---|---|---|---|---|---|
| 1 | 0,013 ± 0,001 | 0,13 | 0,000014 ± 0,000002 | 0,14 | Частично погрузилась |
| 2 | 0,022 ± 0,001 | 0,22 | 0,000020 ± 0,000002 | 0,2 | Полностью погрузилась |
| 3 | 0,028 ± 0,001 | 0,28 | 0,000020 ± 0,000002 | 0,2 | Опустилась на дно |
Вывод: на основе полученных результатов можно сделать выводы, что тело всплывает, если сила тяжести меньше архимедовой силы; тело плавает, если сила тяжести равна архимедовой силе; тело тонет, если сила тяжести больше архимедовой силы.
Добавить текст Вернуть оригиналЛабораторная работа №11. Выяснение условия равновесия рычага
Стр. 220
Цель работы: Проверить на опыте условие равновесия рычага и правило моментов.
Приборы и материалы: Рычаг на штативе, набор грузов массой 100 г каждой, линейкой, динамометр.
Ход работы:
1) Уравновесим рычаг.
2) Подвесим два груза на левой части рычага на расстоянии l1 = 9 см от оси вращения. Чтобы рычаг пришел в горизонтальное равновесное положение, на правой части от оси вращения подвешиваем: а) один груз F2 = 1 Н на расстоянии l2 = 18 см; б) два груза F2 = 2 Н на расстоянии l2 = 9 см; в) три груза F2 = 3 Н на расстоянии l2 = 6 см.
Добавить текст Вернуть оригинал3) Находим отношение сил и плеч: \(\frac{F_{1}}{F_{2}}\) и \(\frac{l_{1}}{l_{2}}\) .
4) Находим моменты сил M1 = F1l1 и M2 = F2l2
Абсолютная погрешность Δl будет равна цене деления линейки, в моем случае Δl = 0,1 см
Добавить текст Вернуть оригинал| № опыта | Сила F1 на левой части рычага, Н |
Плечо l1 ± Δl, см |
Сила F2 на правой части рычага, Н |
Плечо l2 ± Δl, см |
Отношение сил и плеч | Моменты силы | ||
|---|---|---|---|---|---|---|---|---|
| \[\frac{F_{1}}{F_{2}}\] | \[\frac{l_{1}}{l_{2}}\] | M1, Н·м | M2, Н·м | |||||
| 1 | 2 | 9,0 ± 0,1 | 1 | 18,0 ± 0,1 | 2 | 0,5 | 18 | 18 |
| 2 | 2 | 9,0 ± 0,1 | 2 | 9,0 ± 0,1 | 1 | 1 | 18 | 18 |
| 3 | 2 | 9,0 ± 0,1 | 3 | 6,0 ± 0,1 | 0,67 | 1,5 | 18 | 18 |
Вывод: мы на опыте проверили условие равновесия рычага и правило моментов, рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.
Добавить текст Вернуть оригиналДополнительное задание: исследовать равновесие рычага второго рода.
1) На расстоянии l1 = 5 см от оси вращения рычага подвесим 2 груза F1 = 2H.
2) На расстоянии l2 = 20 см от оси вращения правее грузов с помощью динамометра приложим силу равную F2 = 0,5H, чтобы удержать рычаг в равновесии.
Добавить текст Вернуть оригинал| № опыта | Сила F1 на левой части рычага, Н |
Плечо l1 ± Δl, см |
Сила F2 на правой части рычага, Н |
Плечо l2 ± Δl, см |
Отношение сил и плеч | Моменты силы | ||
|---|---|---|---|---|---|---|---|---|
| \[\frac{F_{1}}{F_{2}}\] | \[\frac{l_{1}}{l_{2}}\] | M1, Н·м | M2, Н·м | |||||
| 1 | 2 | 5,0 ± 0,1 | 0,5 | 20,0 ± 0,1 | 4 | 0,25 | 10 | 10 |
Вывод: мы на опыте проверили, что условие равновесия рычага и правило моментов для рычага второго рода так же сохраняется.
Добавить текст Вернуть оригиналЛабораторная работа №12. Определение КПД наклонной плоскости
Стр. 221
Цель работы: Определить коэффициент полезного действия (КПД) наклонной плоскости. Проверить гипотезу: «КПД простого механизма меньше 100% (на примере наклонной плоскости)».
Добавить текст Вернуть оригиналПриборы и материалы: Деревянная доска, динамометр, измерительная лента или линейка, брусок, штатив с муфтой и лапкой.
Ход работы:
1) Определим с помощью динамометра вес бруска: P = 0,46 Н.
Абсолютная погрешность ΔP равна цене деления динамометра: ΔP = 0,02 Н.
Добавить текст Вернуть оригинал2) Высота наклонной плоскости h = 21 см = 0,21 м
Абсолютная погрешность Δh равна цене деления линейки: Δh = 0,1 см = 0,001 м.
Добавить текст Вернуть оригинал3) Полезная работа равна Ап = Ph = 0,46 × 0,21 = 0,097 Дж.
4) Поднимаем брусок по наклонной плоскости с постоянной скоростью. Путь, который проходит брусок, равен: S = 40 см = 0,4 м.
Добавить текст Вернуть оригиналАбсолютная погрешность ΔS равна цене деления линейки: ΔS = 0,1 см = 0,001 м.
Добавить текст Вернуть оригинал5) С помощью динамометра смотрим, какая сила была приложена, чтобы перемещать брусок: F = 0,28 Н.
Абсолютная погрешность ΔF равна цене деления динамометра: ΔF = 0,02 Н.
Добавить текст Вернуть оригинал6) Затраченная работа равна Аз = FS = 0,28 × 0,4 = 0,112 Дж
7) Определяем КПД наклонной плоскости: η = \(\frac{Ап}{Аз}\) × 100% = \(\frac{0,097}{0,112}\) × 100% = 87%
| h1 ± Δh, м | P ± ΔP, H | Ап, Дж | S ± ΔS, м | F ± ΔF, H | Аз, Дж | η, % |
|---|---|---|---|---|---|---|
| 0,210 ± 0,001 | 0,46 ± 0,02 | 0,097 | 0,400 ± 0,001 | 0,28 ± 0,02 | 0,112 | 87 |
Вывод: мы определили коэффициент полезного действия (КПД) наклонной плоскости и на опыте убедились, что полезная работа всегда меньше затраченной и КПД простого механизма всегда меньше 100%.
Добавить текст Вернуть оригинал
