Решебник по алгебре 9 класс Макарычев Задание 869

 

\[\boxed{\text{869\ (869).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Запишем\ номер\ жетонов,\ \]

\[в\ которых\ цифра\ 3\ содержится\ \]

\[один\ раз:\]

\[3,\ 13,\ 23,\ 30,\ 31,\ 32,\ 34,\ 35,\ 36,\ 37,\ \]

\[38,\ 39,\ 43.\]

\[Всего\ получилось\ 13\ номеров.\]

\[Найдем\ вероятность\ того,\ \]

\[что\ вынутый\ жетон\ будет\ \]

\[содержать\ только\ одну\ \]

\[цифру\ 3:\]

\[P = \frac{13}{50} = \frac{26}{100} = 0,26.\]

\[\boxed{\text{869.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[y = f(x) = kx + b \Longrightarrow\]

\[\Longrightarrow линейная\ функция.\]

\[x_{1},\ x_{2} = x_{1} + d,\ x_{3} = x_{1} + 2d \Longrightarrow\]

\[\Longrightarrow арифметическая\ \]

\[прогрессия.\]

\[k,\ b,\ d \Longrightarrow константы.\]

\[f\left( x_{1} \right) = kx_{1} + d;\]

\[f\left( x_{2} \right) = k \cdot \left( x_{1} + d \right) + b =\]

\[= kx_{1} + b + kd;\]

\[f\left( x_{3} \right) = k \cdot \left( x_{1} + 2d \right) + b =\]

\[= kx_{1} + b + 2kd;\]

\[f\left( x_{n} \right) = kx_{1} + b + kd(n - 1).\]

\[Разность\ прогрессии:\]

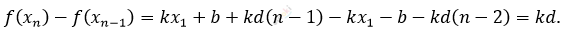
\[\Longrightarrow f\left( x_{1} \right),\ f\left( x_{2} \right),\ldots \Longrightarrow\]

\[\Longrightarrow арифметическая\ \]

\[прогрессия.\]