Решебник по алгебре 9 класс Макарычев Задание 858

 

\[\boxed{\text{858\ (858).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[Найдем,\ сколько\ всего\ \]

\[возможных\ вариантов\ \]

\[открытия\ карточек:\]

\[A_{3}^{4} = 4! = 24.\ Вероятность\ в\ \]

\[каждом\ случае\ будет\ равна:\]

\[\textbf{а)}\ одно\ число - 123:\]

\[\ P = \frac{1}{24};\]

\[\textbf{б)}\ два\ числа - 312\ и\ 321:\ \]

\[P = \frac{2}{24} = \frac{1}{12};\]

\[\textbf{в)}\ количество\ чисел\ с\ первой\ \]

\[цифрой\ 2:\]

\[A_{3}^{2} = 3! = 6.\]

\[P = \frac{6}{24} = \frac{1}{4}.\]

\[\boxed{\text{858.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[\left\{ \begin{matrix} \sqrt[3]{\frac{x}{y}} + \sqrt[3]{\frac{y}{x}} = 4,25 \\ x + y = 130\ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]

\[Пусть\ \ \sqrt[3]{\frac{x}{y}} = a,\ \ тогда:\]

\[a + \frac{1}{a} = 4,25,\ \ \]

\[a^{2} - 4,25a + 1 = 0\]

\[D = {4,25}^{2} - 4 = 14,0625\]

\[a_{1,2} = \frac{4,25 \pm 3,75}{2} \Longrightarrow a_{1} = 4,\ \ \]

\[a_{2} = \frac{1}{4},\]

\[1)\ \left\{ \begin{matrix} \frac{x}{y} = 64\ \ \ \ \ \ \ \ \ \ \\ x + y = 130 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} x = 64y\ \ \ \ \\ 65y = 130 \\ \end{matrix} \right.\ \Longrightarrow\]

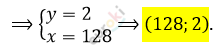
\[2)\ \left\{ \begin{matrix} \frac{x}{y} = \frac{1}{64}\text{\ \ \ \ \ \ \ \ \ \ } \\ x + y = 130 \\ \end{matrix} \right.\ \Longrightarrow\]

\[\Longrightarrow \left\{ \begin{matrix} y = 64x\ \ \ \ \\ 65x = 130 \\ \end{matrix} \right.\ \Longrightarrow\]

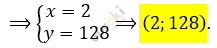
\[Ответ:(128;2);\ \ (2;128).\]