Решебник по алгебре 9 класс Макарычев Задание 855

 

\[\boxed{\text{855\ (855).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ 14C_{n}^{n - 2} = 15A_{n - 3}^{2}\]

\[14 \cdot \frac{n!}{(n - 2)!\left( n - (n - 2) \right)!\ } =\]

\[= 15 \cdot \frac{(n - 3)!}{(n - 3 - 2)!}\]

\[\frac{14n!}{(n - 2)! \cdot 2!} = \frac{15 \cdot (n - 3)!}{(n - 5)!}\]

\[\frac{14 \cdot (n - 1) \cdot n}{2} =\]

\[= \frac{15 \cdot (n - 4)(n - 3)}{1}\]

\[7n^{2} - 7n = 15 \cdot \left( n^{2} - 7n + 12 \right)\]

\[8n^{2} - 98n + 180 = 0\]

\[4n^{2} - 49n + 90 = 0,\ \ n > 0\]

\[D = 2401 - 1440 = 961\]

\[n_{1} = \frac{49 + 31}{8} = 10,\]

\[n_{2} = \frac{49 - 31}{8} = \frac{18}{8} \Rightarrow не\ \]

\[подходит.\]

\[Ответ:n = 10.\]

\[\textbf{б)}\ 6C_{n}^{n - 3} = 11A_{n - 1}^{2}\]

\[\frac{6!}{(n - 3)! \cdot \left( n - (n - 3) \right)!} =\]

\[= \frac{11 \cdot (n - 1)!}{(n - 1 - 2)!}\]

\[\frac{6n!}{(n - 3)! \cdot 3!} = \frac{11 \cdot (n - 1)!}{(n - 3)!}\]

\[n! = 11 \cdot (n - 1)!\]

\[n = 11.\]

\[Ответ:n = 11.\]

\[\textbf{в)}\ 13C_{2n}^{n + 1} = 7C_{2n + 1}^{n - 1}\]

\[\frac{13 \cdot 2n}{(n + 1)! \cdot \left( 2n - (n + 1) \right)!} =\]

\[= \frac{7 \cdot (2n + 1)!}{(n - 1)! \cdot \left( 2n + 1 - (n - 1) \right)!}\]

\[\frac{13 \cdot 2n!}{(n + 1)!(n - 1)!} =\]

\[= \frac{7 \cdot (2n + 1)!}{(n - 1)!(n + 2)!}\]

\[\frac{13}{(n + 1)!} = \frac{7 \cdot (2n + 1)}{(n + 2)!}\]

\[13 = \frac{7 \cdot (2n + 1)}{n + 2}\]

\[13n + 26 = 14n + 7\]

\[n = 19\]

\[Ответ:n = 19.\]

\[\textbf{г)}\ 21C_{2n}^{n + 1} = 11C_{2n + 1}^{n - 1}\]

\[\frac{21 \cdot 2!}{(n + 1)!\left( 2n - (n + 1) \right)!} =\]

\[= \frac{11 \cdot (2n + 1)!}{(n - 1)!\left( 2n + 1 - (n - 1) \right)!}\]

\[\frac{21}{(n + 1)!(n - 1)!} =\]

\[= \frac{11 \cdot (2n + 1)}{(n - 1)! \cdot (n + 2)!}\]

\[21\mathbf{=}\frac{11 \cdot (2n + 1)}{(n + 2)}\]

\[21n + 42 = 22n + 11\]

\[n = 31\]

\[Ответ:n = 31.\]

\[\boxed{\text{855.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[(x + 3)^{4} + (x + 5)^{4} = 4\]

\[Пусть\ \ a = x + 4,\ тогда\]

\[(a - 1)^{4} + (a + 1)^{4} = 4\]

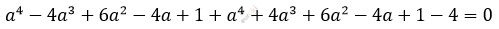
\[2a^{4} + 12a² - 2 = 0\]

\[a^{4} + 6a^{2} - 1 = 0\]

\[Пусть\ a^{2} = c \geq 0,\]

\[c^{2} + 6c - 1 = 0\]

\[D = 9 + 1 = 10\]

\[c = - 3 \pm \sqrt{10},\ \ \]

\[c \geq 0 \Longrightarrow c = \sqrt{10} - 3;\]

\[a = \pm \sqrt{\sqrt{10} - 3},\]

\[\ \ x = a - 4 = \pm \sqrt{\sqrt{10} - 3} - 4.\]

\[Ответ:\ x = \sqrt{\sqrt{10} - 3} - 4;\ \ \ \ \ \ \]

\[\ x = \ - \sqrt{\sqrt{10} - 3} - 4.\]