Алгебра
Английский
Биология
География
Геометрия
История
Русский
Обществознание
Физика
Химия
Информатика
Литература
МатематикаРешебник по алгебре 9 класс Макарычев Задание 853
Задание 853
\[\boxed{\text{853\ (853).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]
\[Пусть\ всего\ \text{x\ }элементов,\ тогда:\]
\[A_{x}^{4} = \frac{x!}{(x - 4)!},\ \ A_{x}^{2} = \frac{x!}{(x - 2)!}.\]
\[По\ условию:\ A_{x}^{4} = 12A_{x}^{2},\]
\[где\ x > 0.\]
\[Составим\ и\ решим\ уравнение:\]
\[\frac{x!}{(x - 4)!} = \frac{12x!}{(x - 2)!}\]
\[12 \cdot (x - 4)! = (x - 2)!\]
\[12 = (x - 3)(x - 2)\]
\[x^{2} - 3x - 2x + 6 - 12 = 0\]
\[x^{2} - 5x - 6 = 0\]
\[D = 25 + 24 = 49\]
\[x_{1} = \frac{5 + 7}{2} = 6\]
\[x_{2} = \frac{5 - 7}{2} = - 1\ \Rightarrow не\ \]
\[подходит.\]
\[Ответ:6\ элементов.\]
\[\boxed{\text{853.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]
\[\left\{ \begin{matrix} x³ - y^{3} = 19 \cdot (x - y) \\ x³ + y³ = 7 \cdot (x + y)\text{\ \ } \\ \end{matrix} \right.\ \]
\[\left\{ \begin{matrix} (x - y)\left( x^{2} + xy + y^{2} \right) = 19 \cdot (x - y) \\ (x + y)\left( x^{2} - xy + y^{2} \right) = 7 \cdot (x + y)\ \\ \end{matrix} \right.\ \]
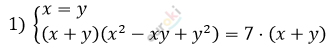
\[\left\{ \begin{matrix} y = x\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} - x^{2} + x^{2} = 7 \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} x^{2} = 7 \\ y = x\ \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} x = \sqrt{7} \\ y = \sqrt{7} \\ \end{matrix} \right.\ \ \ \ или\ \ \left\{ \begin{matrix} x = - \sqrt{7} \\ y = - \sqrt{7} \\ \end{matrix} \right.\ \Longrightarrow\]
\[2)\ \left\{ \begin{matrix} y = - x\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ x^{2} - x^{2} + x^{2} = 19 \\ \end{matrix} \right.\ \Longrightarrow\]
\[\left\{ \begin{matrix} x^{2} = 19 \\ y = - x \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} x = \sqrt{19} \\ y = - \sqrt{19} \\ \end{matrix} \right.\ \text{\ \ }или\ \]
\[\left\{ \begin{matrix} x = - \sqrt{19} \\ y = \sqrt{19}\text{\ \ \ } \\ \end{matrix} \right.\ \Longrightarrow\]
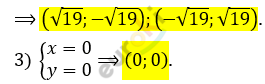
\[4)\ \left\{ \begin{matrix} x^{2} + xy + y^{2} = 19 \\ x^{2} - xy + y^{2} = 7\ \ \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} 2x^{2} + 2y^{2} = 19 + 7 \\ 2xy = 19 - 7\ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} x^{2} + y^{2} = 13 \\ 2xy = 12\ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow\]
\[\Longrightarrow \left\{ \begin{matrix} (x + y)^{2} = 25 \\ xy = 6\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \]
\[1)\ \left\{ \begin{matrix} x + y = 5 \\ xy = 6\ \ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} x = \pm 2 \\ y = \pm 3, \\ \end{matrix} \right.\ \]
\[2)\ \left\{ \begin{matrix} x + y = - 5 \\ xy = 6\ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} x = \pm 3 \\ y = \pm 2. \\ \end{matrix} \right.\ \]
