Решебник по алгебре 9 класс Макарычев Задание 691

 

\[\boxed{\text{691}\text{\ (691)}\text{.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ Сначала\ надо\ найти\ сумму\ всех\ чисел,\ которые\ меньше\ 100\ \]

\[и\ кратны\ 3:\]

\[a_{1} = 3,\ \ d = 3,\]

\[a_{n} = a_{1} + d(n - 1) = 3 + 3n - 3 = 3n\]

\[3n = 99 \Longrightarrow n = 33,\]

\[S_{33} = \frac{a_{1} + a_{33}}{2} \cdot 33 = 51 \cdot 33 = 1683.\]

\[Теперь\ узнаем\ сумму\ чисел,\ которые\ меньше\ 100:\]

\[S_{99} = \frac{a_{1} + a_{99}}{2} \cdot 99 = 4950.\]

\[Найдем\ разность:\]

\[S_{99} - S_{33} = 4950 - 1683 = 3267.\]

\[\textbf{б)}\ Узнаем,\ чему\ равна\ сумма\ чисел,\ которые\ больше\ 50,\ но\]

\[меньше\ 150\ и\ кратны\ 5:\]

\[a_{1} = 55,\ \ d = 5.\]

\[a_{n} = a_{1} + d(n - 1) = 55 - 5n - 5 = 50 - 5n\]

\[50 - 5n = 145 \Longrightarrow n = 19.\]

\[S_{19} = \frac{a_{1} + a_{19}}{2} \cdot 19 = \frac{200}{2} \cdot 19 = 1900.\]

\[Узнаем,\ чему\ равна\ сумма\ чисел,\ которые\ больше\ 50,\ но\ меньше,\]

\[чем\ 150:\]

\[a_{1} = 51,\ \ d = 1,\]

\[a_{n} = a_{1} + d(n - 1) = 51 + n - 1 = 50 + n\]

\[50 + n = 149 \Longrightarrow n = 99.\]

\[S_{99} = \frac{a_{1} + a_{99}}{2} \cdot 99 = \frac{200}{2} \cdot 99 = 9900.\]

\[Осталось\ посчитать\ разность:\]

\[S = S_{99} - S_{19} = 9900 - 1900 = 8000.\]

\[\boxed{\text{691.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[\textbf{а)}\ 3x^{2} - 6x - 5\ \ \ \ \]

\[при\ x = 1 + \sqrt{2}:\]

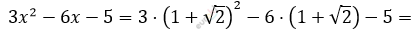
\[= 3 + 6\sqrt{2} + 6 - 6 - 6\sqrt{2} - 5 =\]

\[= - 2.\]

\[\textbf{б)}\ \frac{x^{2} - x - 5}{x - 1}\]

\[при\ x = \sqrt{5} + 1:\]

\[\frac{x^{2} - x - 5}{x - 1} =\]

\[= \frac{\left( \sqrt{5} + 1 \right)^{2} - \left( \sqrt{5} + 1 \right) - 5}{\sqrt{5} + 1 - 1} =\]

\[= \frac{5 + 2\sqrt{5} + 1 - \sqrt{5} - 1 - 5}{\sqrt{5}} =\]

\[= \frac{\sqrt{5}}{\sqrt{5}} = 1.\]