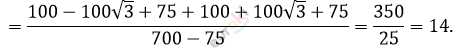Решебник по алгебре 9 класс Макарычев Задание 687

 

\[\boxed{\text{687}\text{\ (687)}\text{.}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ d = - 0,4,\ \ n = 12,\ \ a_{n} = 2,4 \Longrightarrow\]

\[a_{n} = a_{1} + d \cdot (n - 1)\]

\[2,4 = a_{1} - 0,4 \cdot (12 - 1)\]

\[2,4 = a_{1} - 4,4\]

\[a_{1} = 6,8\]

\[S_{12} = \frac{a_{1} + a_{12}}{2} \cdot 12 = (6,8 + 2,4) \cdot 6 = 55,2.\]

\[\textbf{б)}\ a_{1} = - 35,\ \ d = 5,\ \ S = 250 \Longrightarrow\]

\[S_{n} = \frac{2a_{1} + d(n - 1)}{2} \cdot n = \frac{- 70 + 5n - 5}{2} \cdot n = 250\]

\[- 75n + 5n^{2} = 100\]

\[n^{2} - 15n - 100 = 0\]

\[D = 15^{2} + 4 \cdot 100 = 625\]

\[n = \frac{15 \pm 25}{2} = 20;\ - 5;так\ как\ n > 0,\ то\ n = 20;\]

\[a_{20} = a_{1} + d(n - 1) = - 35 + 5 \cdot 19 = 60.\]

\[\textbf{в)}\ d = \frac{1}{2},\ \ a_{n} = 50,\ \ S_{n} = 2525 \Longrightarrow\]

\[S_{n} = \frac{a_{1} + 50}{2} \cdot n = 2525\]

\[n\left( a_{1} + 50 \right) = 5050\]

\[\left\{ \begin{matrix} a_{1} + 0,5 \cdot (n - 1) = 50 \\ n\left( a_{1} + 50 \right) = 5050\ \ \ \ \ \\ \end{matrix} \right.\ \Longrightarrow \left\{ \begin{matrix} a_{1} = 50,5 - 0,5n\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ n(50,5 - 0,5n + 50) = 5050 \\ \end{matrix} \right.\ \]

\[\Longrightarrow 0,5n^{2} - 100,5n + 5050 = 0 \Longrightarrow n^{2} - 201n + 10100 = 0 \Longrightarrow\]

\[D = 201^{2} - 4 \cdot 10100 = 1\]

\[n = \frac{201 \pm 1}{2},\ \ n_{1} = 100,\ \ n_{2} = 101;\]

\[1)\ если\ \ n = 100,\ \ a_{1} = a_{n} - d(n - 1) = 50 - \frac{1}{2} \cdot 99 = 0,5;\]

\[2)\ если\ n = 101,\ \ a_{1} = a_{n} - d(n - 1) = 50 - \frac{1}{2} \cdot 100 = 0;\]

\[\textbf{г)}\ a_{1} = - \frac{1}{2},\ \ a_{n} = a_{1} + d(n - 1) = - 0,5 + d(n - 1) = - 29\frac{1}{2};\]

\[S_{n} = \frac{a_{1} + a_{n}}{2} \cdot n = \frac{- \frac{1}{2} - 29\frac{1}{2}}{2} \cdot n = - 450;\]

\[\Longrightarrow - \frac{30}{2} \cdot n = - 450,\ \ n = 30,\]

\[\Longrightarrow - 0,5 + 29d = - 29,5\]

\[29d = - 29\]

\[d = - 1.\]

\[\boxed{\text{687.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[\textbf{а)}\ \left( \sqrt{15} + \sqrt{10} \right) \cdot 2\sqrt{5} - 5\sqrt{12} =\]

\[= \left( \sqrt{15} + \sqrt{10} \right) \cdot \sqrt{20} - \sqrt{300} =\]

\[= \sqrt{300} + \sqrt{200} - \sqrt{300} =\]

\[= \sqrt{200} = 10\sqrt{2};\]

\[\textbf{б)}\ \frac{2\sqrt{70} - 2\sqrt{28}}{3\sqrt{35} - 3\sqrt{14}} =\]

\[= \frac{2\sqrt{2} \cdot (\sqrt{35} - \sqrt{14})}{3 \cdot (\sqrt{35} - \sqrt{14})} = \frac{2\sqrt{2}}{3};\]

\[\textbf{в)}\ \left( 2\sqrt{12} - 3\sqrt{3} \right)^{2} =\]

\[= \left( 4\sqrt{3} - 3\sqrt{3} \right)^{2} = 3;\]

\[\textbf{г)}\ \frac{10 - 5\sqrt{3}}{10 + 5\sqrt{3}} + \frac{10 + 5\sqrt{3}}{10 - 5\sqrt{3}} =\]

\[= \frac{\left( 10 - 5\sqrt{3} \right)^{2} \cdot \left( 10 + 5\sqrt{3} \right)^{2}}{\left( 10 + 5\sqrt{3} \right)\left( 10 - 5\sqrt{3} \right)} =\]