Решебник по алгебре 9 класс Макарычев Задание 520

\[\boxed{\text{520\ (520).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ \frac{y - x}{x - 2} = 0 \Longrightarrow y = x,\ \ x \neq 2.\]

\[\textbf{б)}\ \frac{y - x^{2}}{x^{2} - 1} = 0 \Longrightarrow y = x^{2},\]

\[x \neq \pm 1.\]

\[\textbf{в)}\ \frac{x^{2} + y^{2} - 16}{y^{2} - 4} = 0 \Longrightarrow\]

\[\Longrightarrow x^{2} + y^{2} = 16,\ \ y \neq \pm 2.\]

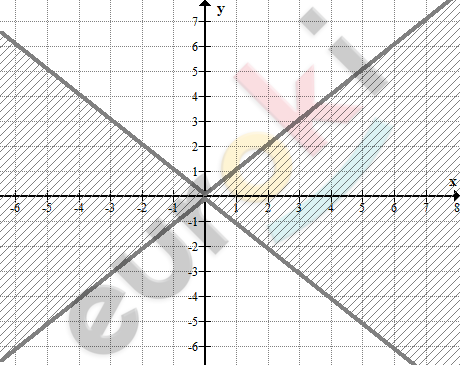
\[\textbf{г)}\ \frac{x^{2} + y^{2} - 1}{x^{2} - y^{2}} = 0 \Longrightarrow x^{2} + y^{2} =\]

\[= 1 \Longrightarrow y \neq \pm x.\]

\[\boxed{\text{520.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

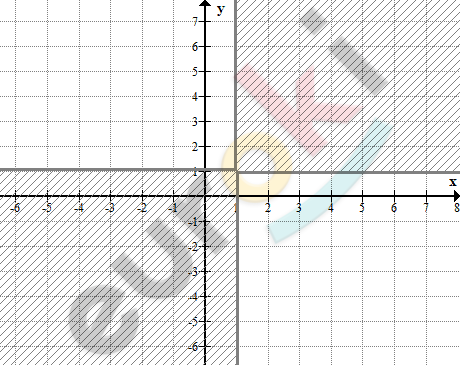
\[\textbf{а)}\ (x - 1)(y - 1) \geq 0\]

\[\textbf{б)}\ x² - y^{2} > 0\]