Решебник по алгебре 9 класс Макарычев Задание 361

 

\[\boxed{\text{361\ (361).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

\[\textbf{а)}\ x^{4} - 9x^{2} + 18 = 0\]

\[Пусть\ x^{2} = t;\ t \geq 0:\]

\[t^{2} - 9t + 18 = 0\]

\[D = 81 - 4 \cdot 18 = 9\]

\[t_{1,2} = \frac{9 \pm 3}{2} = 3;6.\]

\[1)\ x^{2} = 3\ \ \]

\[x_{1,2} = \pm \sqrt{3}.\]

\[2)\ x^{2} = 6\]

\[x_{3,4} = \pm \sqrt{6}.\]

\[Сумма\ корней:\]

\[\sqrt{3} - \sqrt{3} + \sqrt{6} - \sqrt{6} = 0.\]

\[Ответ:0.\]

\[\textbf{б)}\ x^{4} + 3x^{2} - 10 = 0\]

\[Пусть\ x^{2} = t;\ \ t \geq 0:\]

\[t^{2} + 3t - 10 = 0\]

\[D = 9 + 4 \cdot 10 = 49\]

\[t_{1,2} = \frac{- 3 \pm 7}{2} = - 5;2;\ \ \]

\[так\ как\ t \geq 0,\ то\ t = 2:\]

\[x^{2} = 2\ \ \]

\[x_{1,2} = \pm \sqrt{2}.\]

\[Сумма\ корней:\]

\[x_{1} + x_{2} = \sqrt{2} - \sqrt{2} = 0.\]

\[Ответ:0.\]

\[\textbf{в)}\ 4x^{4} - 12x^{2} + 1 = 0\]

\[Пусть\ t = x^{2};\ \ t \geq 0:\]

\[4t^{2} - 12t + 1 = 0\]

\[D_{1} = 36 - 4 = 32\]

\[t_{1,2} = \frac{6 \pm \sqrt{32}}{4} =\]

\[= \frac{6 \pm 4\sqrt{2}}{4} = \frac{3 \pm \sqrt{2}}{2}.\]

\[1)\ x^{2} = \frac{3 + \sqrt{2}}{2}\ \]

\[x_{1,2} = \pm \sqrt{\frac{3 + \sqrt{2}}{2}};\]

\[2)\ x^{2} = \frac{3 - \sqrt{2}}{2}\]

\[\ x_{3,4} = \pm \sqrt{\frac{3 - \sqrt{2}}{2}}.\]

\[Сумма\ корней:\]

\[x_{1} + x_{2} + x_{3} + x_{4} = \sqrt{\frac{3 + \sqrt{2}}{2}} -\]

\[- \sqrt{\frac{3 + \sqrt{2}}{2}} + \sqrt{\frac{3 - \sqrt{2}}{2}} -\]

\[- \sqrt{\frac{3 - \sqrt{2}}{2}} = 0.\]

\[Ответ:0.\]

\[\textbf{г)}\ 12y^{4} - y^{2} - 1 = 0\]

\[Пусть\ \ t = y^{2};\ \ \ t \geq 0:\]

\[12t^{2} - t - 1 = 0\]

\[D = 1 + 4 \cdot 12 = 49\]

\[t_{1,2} = \frac{1 \pm 7}{24} = - \frac{1}{4};\ \frac{1}{3}.\]

\[так\ как\ t \geq 0,\ то\ t = \frac{1}{3}:\]

\[y^{2} = \frac{1}{3}\]

\[y_{1,2} = \pm \sqrt{\frac{1}{3}}.\]

\[Сумма\ корней:\]

\[y_{1} + y_{2} = \sqrt{\frac{1}{3}} - \sqrt{\frac{1}{3}} = 0.\]

\[Ответ:0.\]

\[\boxed{\text{361.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

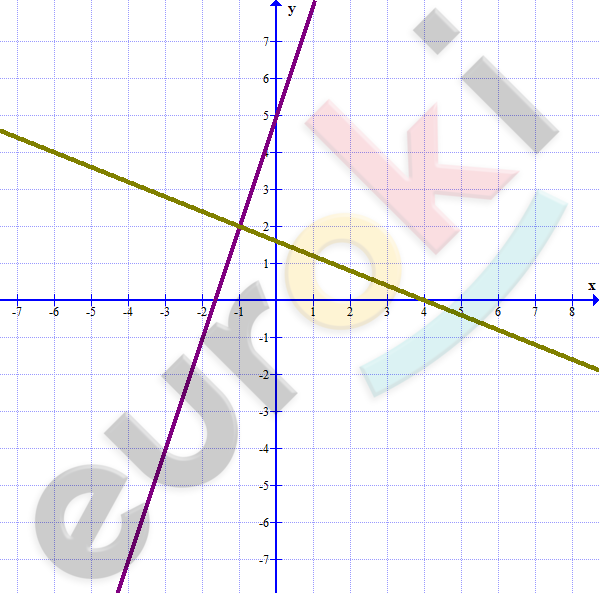
\[Вторая\ координатная\ \]

\[четверть.\]

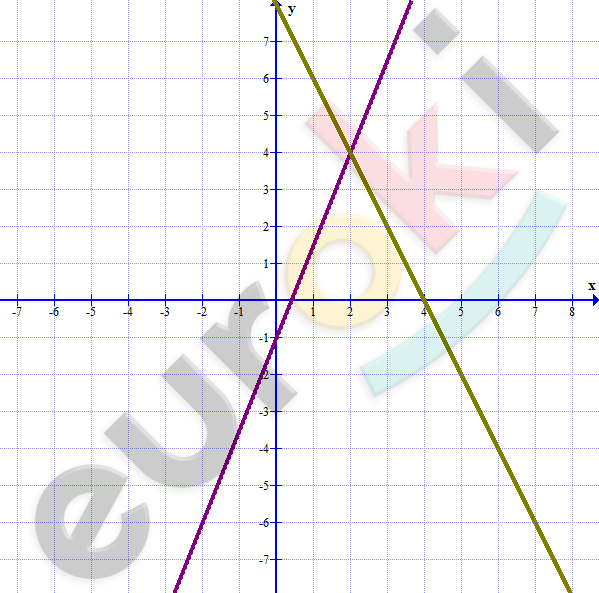
\[Первая\ координатная\ \]

\[четверть.\]