Решебник по алгебре 9 класс Макарычев Задание 190

 

\[\boxed{\text{190\ (190).}\text{\ }\text{Еуроки\ -\ ДЗ\ без\ мороки}}\]

Пояснение.

Решение.

\[\textbf{а)}\ 3^{\frac{1}{2}} = \sqrt{3};\ \ \ \]

\[\ 5^{\frac{3}{4}} = \left( 5^{3} \right)^{\frac{1}{4}} = \sqrt[4]{5^{3}} = \sqrt[4]{125};\ \ \ \]

\[{0,2}^{0,5} = {0,2}^{\frac{1}{2}} = \sqrt{0,2};\]

\[7^{- 0,25} = \left( \frac{1}{7} \right)^{\frac{1}{4}} = \sqrt[4]{\frac{1}{7}};\]

\[\textbf{б)}\ x^{\frac{3}{4}} = \left( x^{3} \right)^{\frac{1}{4}} = \sqrt[4]{x^{3}};\ \ \ \]

\[a^{1,2} = a^{\frac{5}{6}} = \sqrt[5]{a^{6}};\ \ \ \]

\[b^{- 0,8} = \left( \frac{1}{b} \right)^{\frac{4}{5}} = \sqrt[5]{\frac{1}{b^{4}}};\]

\[c^{2\frac{2}{3}} = c^{\frac{8}{3}} = \sqrt[3]{c^{8}};\ \]

\[\textbf{в)}\ 5a^{\frac{1}{3}} = 5\sqrt[3]{a};\ \ \ \]

\[ax^{\frac{3}{5}} = a\sqrt[5]{x^{3}};\ \]

\[- b^{- 1,5} = - \left( \frac{1}{b} \right)^{\frac{3}{2}} = - \frac{1}{\sqrt{b^{3}}};\ \ \]

\[(2b)^{\frac{1}{4}} = \sqrt[4]{2b};\]

\[\textbf{г)}\ (x - y)^{\frac{2}{3}} = \sqrt[3]{(x - y)^{2}};\ \ \ \]

\[x^{\frac{2}{3}} - y^{\frac{2}{3}} = \sqrt[3]{x^{2}} - \sqrt[3]{y^{2}}\ ;\]

\[3 \cdot (a + b)^{\frac{3}{4}} = 3\sqrt[4]{(a + b)^{3}};\ \ \]

\[\ 4a^{- \frac{2}{3}} + ax^{\frac{2}{3}} = \frac{4}{\sqrt[3]{a^{2}}} + a\sqrt[3]{x^{2}.}\ \]

\[\boxed{\text{190.}\text{\ }\text{ОК\ ГДЗ\ -\ домашка\ на\ 5}}\]

\[\textbf{а)}\ f(x) = \frac{x^{2} - 9}{x - 3} =\]

\[= \frac{(x - 3)(x + 3)}{x - 3} = x + 3;\ \ \]

\[\ \ x \neq 3.\]

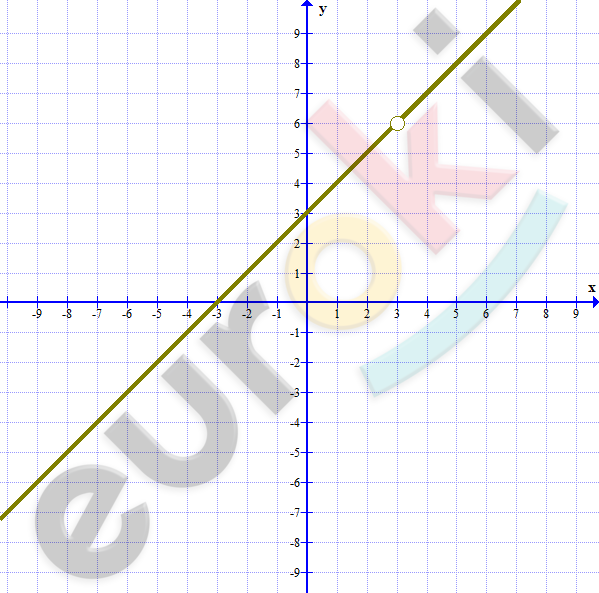
\[D(f) = ( - \infty;3) \cup (3; + \infty).\]

\[E(f) = ( - \infty;6) \cup (6; + \infty).\]

\[Нули\ функции:\ \ x = - 3.\]

\[f(x) > 0\ при\ \]

\[x \in ( - 3;3) \cup (3; + \infty);\]

\[f(x) < 0\ при\ x < - 3.\]

\[Возрастает\ на\ промежутке\ \]

\[( - \infty;3) \cup (3; + \infty).\]

\[Не\ имеет\ наибольшего\ и\ \]

\[наименьшего\ значений.\]

\[Ни\ четная,\ ни\ нечетная.\]

\[\textbf{б)}\ f(x) = \frac{x^{2} - 6x - 7}{x + 1} =\]

\[= \frac{(x + 1)(x - 7)}{x + 1} = x - 7;\ \]

\[\ \ x \neq - 1.\]

\[x^{2} - 6x - 7 = (x + 1)(x - 7)\]

\[x_{1} + x_{2} = 6;\ \ \ x_{1} \cdot x_{2} = - 7\]

\[x_{1} = 7;\ \ \ \ x_{2} = - 1.\]

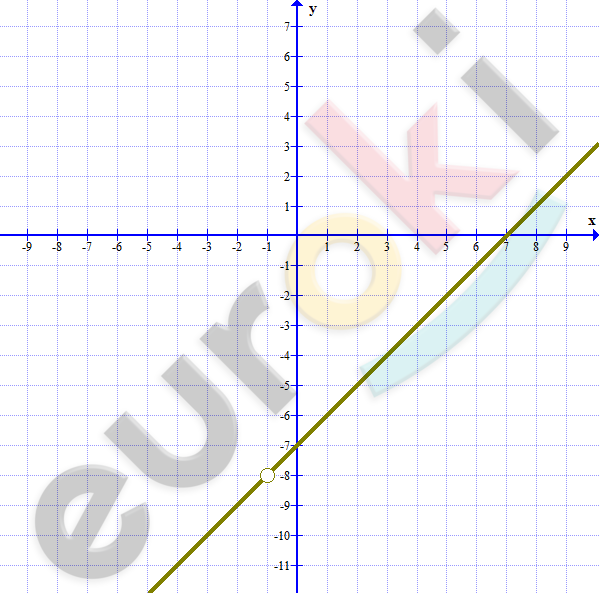
\[D(f) = ( - \infty; - 1) \cup ( - 3; + \infty).\]

\[E(f) = ( - \infty; - 8) \cup ( - 8; + \infty).\]

\[Нули\ функции:\ \ x = 7.\]

\[f(x) > 0\ при\ x > 7;\]

\[f(x) < 0\ при\ \]

\[x \in ( - \infty; - 1) \cup ( - 1;7).\]

\[Возрастает\ на\ промежутке\]

\[\ ( - \infty; - 1) \cup ( - 1; + \infty).\]

\[Не\ имеет\ наибольшего\ и\ \]

\[наименьшего\ значений.\]

\[Ни\ четная,\ ни\ нечетная.\]