Решебник по алгебре 9 класс Мерзляк Задание 762

 

\[\boxed{\mathbf{762\ (762).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[Пусть\ x\ \frac{дет}{д} - план\ \]

\[рабочего,\ а\ (x + 8)\ \frac{дет}{д} - он\ \]

\[стал\ делать.\ Тогда\ \]

\[за\ 3\ дня\ он\ сделал\ 3x\ деталей,\]

\[\ \left( \frac{216}{x} \right) - время,\ за\ которое\ \]

\[должно\ было\ \]

\[быть\ готово\ 216\ деталей.\ \]

\[Составляем\ уравнение:\]

\[3x + \left( \frac{216}{x} - 4 \right)(x + 8) = 232\ \ \ \ \]

\[| \cdot x \neq 0\]

\[3x^{2} + (216 - 4x)(x + 8) -\]

\[- 232x = 0\]

\[3x^{2} + 216x + 1728 - 4x^{2} -\]

\[- 32x - 232x = 0\]

\[- x^{2} - 48x + 1728 = 0\ \ \ | \cdot ( - 1)\]

\[x^{2} + 48x - 1728 = 0\]

\[D = 2304 + 6912 = 9216\]

\[x_{1} = \frac{- 48 + 96}{2} = 24;\ \ \ \ \]

\[\ x_{2} = \frac{- 48 - 96}{2} < 0\ \ \]

\[24\ детали\ должен\ был\]

\[\ изготавливать\ рабочий.\]

\[Ответ:24\ детали.\]

\[\boxed{\mathbf{762.\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

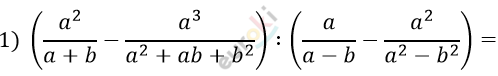
\[= \frac{\text{ab}(a - b)}{a^{2} + ab + b^{2}}\]

\[\frac{{a^{2}}^{\backslash a^{2} + ab + b^{2}}}{a + b} - \frac{{a^{3}}^{\backslash a + b}}{a^{2} + ab + b^{2}} =\]

\[= \frac{a^{4} + a^{3}b + a^{2}b^{2} - a^{4} - a^{3}b}{(a + b)\left( a^{2} + ab + b^{2} \right)} =\]

\[= \frac{a^{2}b^{2}}{(a + b)\left( a^{2} + ab + b^{2} \right)}\]

\[\frac{a^{\backslash a + b}}{a - b} - \frac{a^{2}}{a^{2} - b^{2}} =\]

\[= \frac{a^{2} + ab - a^{2}}{(a - b)(a + b)} = \frac{\text{ab}}{a^{2} - b^{2}}\]

\[\frac{a^{2}b^{2}}{(a + b)\left( a^{2} + ab + b^{2} \right)} \cdot \frac{(a - b)(a + b)}{\text{ab}} =\]

\[= \frac{\text{ab}(a - b)}{a^{2} + ab + b^{2}}\]

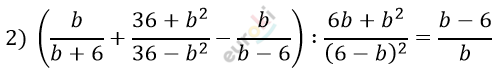
\[\frac{b^{\backslash b - 6}}{b + 6} - \frac{36 + b^{2}}{b^{2} - 36} - \frac{b^{\backslash b + 6}}{b - 6} =\]

\[= \frac{b^{2} - 6b - 36 - b^{2} - b^{2} - 6b}{(b - 6)(b + 6)} =\]

\[= - \frac{b^{2} + 12b + 36}{(b - 6)(b + 6)} =\]

\[= \frac{(b + 6)^{2}}{(6 - b)(b + 6)} = \frac{b + 6}{6 - b}\]

\[\frac{b + 6}{6 - b} \cdot \frac{(6 - b)^{2}}{b(6 + b)} = \frac{b - 6}{b}.\]