Решебник по алгебре 9 класс Мерзляк Задание 753

 

\[\boxed{\mathbf{753\ (753).\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[a_{1} = 3x + 4,\ \ a_{2} = 2x + 3,\]

\[\text{\ \ }a_{3} = x^{2},\ \ a_{4} = 2x^{2} + x\]

\[a_{1} + a_{4} = a_{3} + a_{2}\]

\[3x + 4 + 2x^{2} + x = 2x + 3 + x^{2}\]

\[x^{2} + 2x + 1 = 0\]

\[(x + 1)^{2} = 0\]

\[x = - 1\]

\[При\ x = - 1:\ \]

\[a_{1} = - 3 + 4 = 1,\ \ \]

\[a_{2} = - 2 + 3 = 1,\ \ a_{3} = 1,\ \ \]

\[a_{4} = 2 \cdot 1 - 1 = 1\]

\[Ответ:x = - 1 \Longrightarrow \ a_{1} = 1,\]

\[\ a_{2} = 1,\ a_{3} = 1,\ a_{4} = 1.\]

\[\boxed{\mathbf{753.\ }Еуроки\ - \ ДЗ\ без\ мороки}\]

\[y =\]

\[= \underset{\begin{matrix} бесконечная\ геометрическая\ \\ прогрессия \\ \end{matrix}}{\overset{x^{2} + \frac{x^{2}}{1 + x^{2}} + \frac{x^{2}}{\left( 1 + x^{2} \right)^{2}} + \ldots}{︸}},\ \]

\[\ x \neq 0\]

\[q = \frac{x^{2}}{1 + x^{2}}\ \ :x^{2} = \frac{1}{1 + x^{2}}\]

\[S = \frac{x^{2}}{1 - \frac{1}{1 + x^{2}}} = \frac{x^{2}}{\frac{1 + x^{2} - 1}{1 + x^{2}}} =\]

\[= \frac{x^{2}\left( 1 + x^{2} \right)}{x^{2}} = 1 + x^{2};\ \ x \neq 0\]

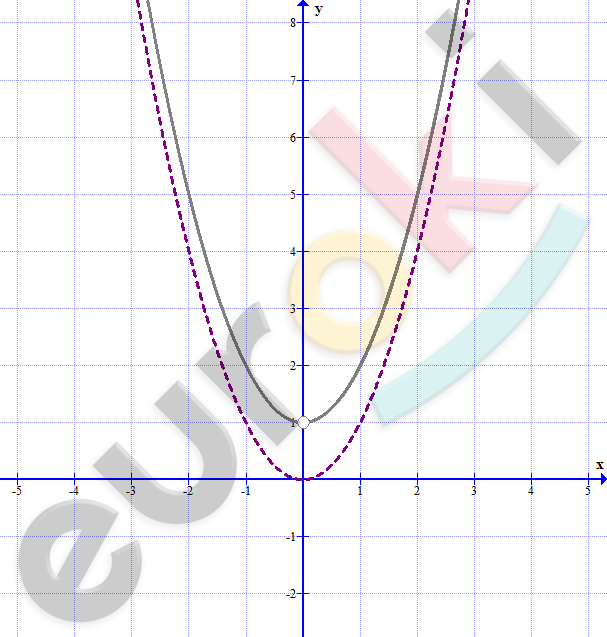
\[y = x^{2} + 1;\ \ x \neq 0\ \]

\[график\ y = x^{2}\ перенести\ на\ \]

\[1\ единицу\ вверх.\]